
Question Number 218208 by Marzuk last updated on 01/Apr/25
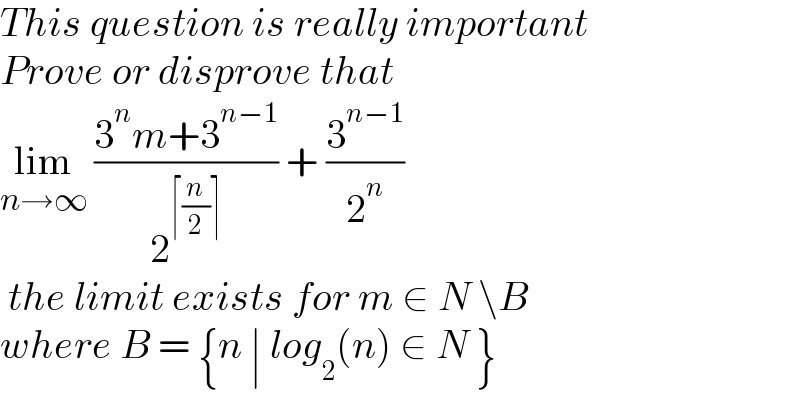
$${This}\:{question}\:{is}\:{really}\:{important} \\ $$$${Prove}\:{or}\:{disprove}\:{that} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{3}^{{n}} {m}+\mathrm{3}^{{n}−\mathrm{1}} }{\mathrm{2}^{\lceil\frac{{n}}{\mathrm{2}}\rceil} }\:+\:\frac{\mathrm{3}^{{n}−\mathrm{1}} }{\mathrm{2}^{{n}} }\: \\ $$$$\:{the}\:{limit}\:{exists}\:{for}\:{m}\:\in\:{N}\:\backslash{B} \\ $$$${where}\:{B}\:=\:\left\{{n}\:\mid\:{log}_{\mathrm{2}} \left({n}\right)\:\in\:{N}\:\right\} \\ $$
Commented by Marzuk last updated on 01/Apr/25
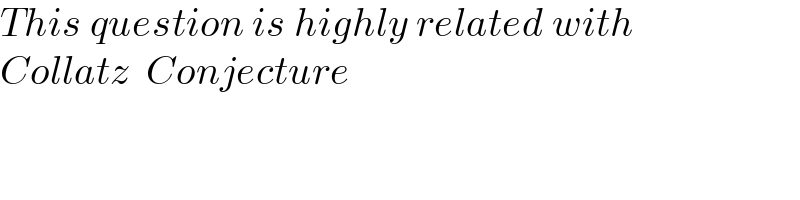
$${This}\:{question}\:{is}\:{highly}\:{related}\:{with} \\ $$$${Collatz}\:\:{Conjecture} \\ $$
Answered by MrGaster last updated on 05/Apr/25
![=lim_(n→∞) ((3^(n−1) (3m+1))/2^([n/2]) )+(3^(n−1) /2^n ) =lim_(n→∞) 3^(n−1) (((3m+1)/2^([n/2]) )+(1/2^n )) ∀n∈N,[(n/2)]is defined as ⌈(n/2)⌉= { (((n/2) if n∈even)),((((n+1)/2) if n is odd)) :} Case when n is even: 2^(⌈(n/2)⌉) =2^(n/2) ⇒((3^(n−1) (3m+1))/2^(n/2) )=((3^n (3m+1))/(3∙2^(n/2) ))=(((3m+1))/3)∙((9/2))^(n/2) n∈odd: 2^(⌈(n/2)⌉) =2^((n+1)/2) ⇒((3^(n−1) (3m+1))/2^((n+1)/2) )=((3^n (3m+1))/(3∙2^((n+1)/3) ))=(((3m+1))/(3(√2)))∙((9/2))^(n/2) Second term: (3^(n−1) /2^n )=(1/3)∙((3/4))^n Main term analysis (order comparison): ((9/2))^(n/2) ≫((3/4))^n ∵((9/2))^(1/2) =(3/( (√2)))>(3/4) ⇒lim_(n→∞) (((3m+1)/3)∙((9/2))^(n/2) +(1/3)∙((3/4))^n )=+∞ ⇒∄lim](Q218285.png)
$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{3}^{{n}−\mathrm{1}} \left(\mathrm{3}{m}+\mathrm{1}\right)}{\mathrm{2}^{\left[{n}/\mathrm{2}\right]} }+\frac{\mathrm{3}^{{n}−\mathrm{1}} }{\mathrm{2}^{{n}} } \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}3}^{{n}−\mathrm{1}} \left(\frac{\mathrm{3}{m}+\mathrm{1}}{\mathrm{2}^{\left[{n}/\mathrm{2}\right]} }+\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right)\:\forall{n}\in\mathbb{N},\left[\frac{{n}}{\mathrm{2}}\right]\mathrm{is}\:\mathrm{defined}\:\mathrm{as} \\ $$$$\lceil\frac{{n}}{\mathrm{2}}\rceil=\begin{cases}{\frac{{n}}{\mathrm{2}}\:\mathrm{if}\:{n}\in\mathrm{even}}\\{\frac{{n}+\mathrm{1}}{\mathrm{2}}\:\mathrm{if}\:{n}\:\mathrm{is}\:\mathrm{odd}}\end{cases} \\ $$$$\mathrm{Case}\:\mathrm{when}\:{n}\:\mathrm{is}\:\mathrm{even}: \\ $$$$\mathrm{2}^{\lceil\frac{{n}}{\mathrm{2}}\rceil} =\mathrm{2}^{{n}/\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{3}^{{n}−\mathrm{1}} \left(\mathrm{3}{m}+\mathrm{1}\right)}{\mathrm{2}^{{n}/\mathrm{2}} }=\frac{\mathrm{3}^{{n}} \left(\mathrm{3}{m}+\mathrm{1}\right)}{\mathrm{3}\centerdot\mathrm{2}^{{n}/\mathrm{2}} }=\frac{\left(\mathrm{3}{m}+\mathrm{1}\right)}{\mathrm{3}}\centerdot\left(\frac{\mathrm{9}}{\mathrm{2}}\right)^{{n}/\mathrm{2}} \\ $$$${n}\in\mathrm{odd}: \\ $$$$\mathrm{2}^{\lceil\frac{{n}}{\mathrm{2}}\rceil} =\mathrm{2}^{\left({n}+\mathrm{1}\right)/\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{3}^{{n}−\mathrm{1}} \left(\mathrm{3}{m}+\mathrm{1}\right)}{\mathrm{2}^{\left({n}+\mathrm{1}\right)/\mathrm{2}} }=\frac{\mathrm{3}^{{n}} \left(\mathrm{3}{m}+\mathrm{1}\right)}{\mathrm{3}\centerdot\mathrm{2}^{\left({n}+\mathrm{1}\right)/\mathrm{3}} }=\frac{\left(\mathrm{3}{m}+\mathrm{1}\right)}{\mathrm{3}\sqrt{\mathrm{2}}}\centerdot\left(\frac{\mathrm{9}}{\mathrm{2}}\right)^{{n}/\mathrm{2}} \\ $$$$\mathrm{Second}\:\mathrm{term}: \\ $$$$\frac{\mathrm{3}^{{n}−\mathrm{1}} }{\mathrm{2}^{{n}} }=\frac{\mathrm{1}}{\mathrm{3}}\centerdot\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{{n}} \\ $$$$\mathrm{Main}\:\mathrm{term}\:\mathrm{analysis}\:\left(\mathrm{order}\:\mathrm{comparison}\right): \\ $$$$\left(\frac{\mathrm{9}}{\mathrm{2}}\right)^{{n}/\mathrm{2}} \gg\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{{n}} \because\left(\frac{\mathrm{9}}{\mathrm{2}}\right)^{\mathrm{1}/\mathrm{2}} =\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}>\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{3}{m}+\mathrm{1}}{\mathrm{3}}\centerdot\left(\frac{\mathrm{9}}{\mathrm{2}}\right)^{{n}/\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{3}}\centerdot\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{{n}} \right)=+\infty \\ $$$$\Rightarrow\nexists\underline{\mathrm{lim}} \\ $$
