
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 114797 by bemath last updated on 21/Sep/20

$${There}\:{are}\:\mathrm{6}\:{people}\:{going}\:{to}\:{sit}\:{in}\: \\ $$$${a}\:{circle}\:.\:{The}\:{number}\:{of}\:{arrangements} \\ $$$${they}\:{sit}\:{if}\:{there}\:{are}\:\mathrm{2}\:{people}\:{who} \\ $$$${always}\:{sit}\:{next}\:{to}\:{each}\:{other} \\ $$
Answered by mr W last updated on 21/Sep/20

$$\mathrm{2}×\mathrm{4}!=\mathrm{48} \\ $$
Commented by bemath last updated on 21/Sep/20

$${gave}\:{kudos} \\ $$
Commented by bemath last updated on 21/Sep/20
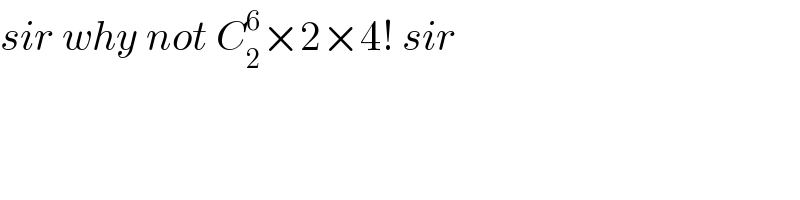
$${sir}\:{why}\:{not}\:{C}_{\mathrm{2}} ^{\mathrm{6}} ×\mathrm{2}×\mathrm{4}!\:{sir} \\ $$
Commented by mr W last updated on 21/Sep/20

$${we}\:{have}\:{always}\:{two}\:{people}\:{next}\:{to} \\ $$$${each}\:{other}.\:{here}\:{it}\:{is}\:{meant}\:{that}\:{two} \\ $$$${particular}\:{people}\:{are}\:{next}\:{to}\:{each} \\ $$$${other},\:{so}\:{you}\:{can}\:{not}\:{select}\:{two}\:{any} \\ $$$${people}\:{from}\:\mathrm{6}. \\ $$
Commented by bemath last updated on 21/Sep/20
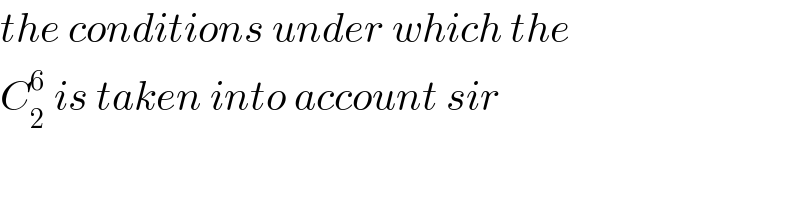
$${the}\:{conditions}\:{under}\:{which}\:{the}\: \\ $$$${C}_{\mathrm{2}} ^{\mathrm{6}} \:{is}\:{taken}\:{into}\:{account}\:{sir} \\ $$
Commented by mr W last updated on 21/Sep/20
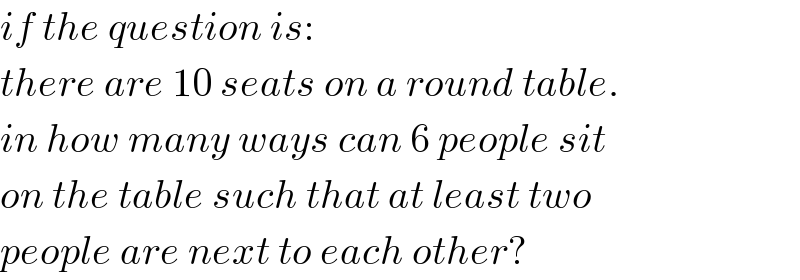
$${if}\:{the}\:{question}\:{is}: \\ $$$${there}\:{are}\:\mathrm{10}\:{seats}\:{on}\:{a}\:{round}\:{table}. \\ $$$${in}\:{how}\:{many}\:{ways}\:{can}\:\mathrm{6}\:{people}\:{sit} \\ $$$${on}\:{the}\:{table}\:{such}\:{that}\:{at}\:{least}\:{two} \\ $$$${people}\:{are}\:{next}\:{to}\:{each}\:{other}? \\ $$
Commented by bemath last updated on 21/Sep/20
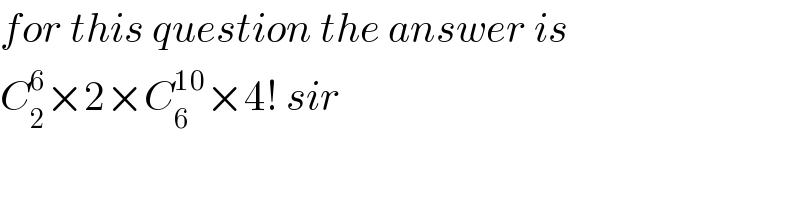
$${for}\:{this}\:{question}\:{the}\:{answer}\:{is}\: \\ $$$${C}_{\mathrm{2}} ^{\mathrm{6}} ×\mathrm{2}×{C}_{\mathrm{6}} ^{\mathrm{10}} ×\mathrm{4}!\:{sir} \\ $$
Commented by mr W last updated on 21/Sep/20

$${C}_{\mathrm{2}} ^{\mathrm{6}} ×\mathrm{2}×{C}_{\mathrm{4}} ^{\mathrm{8}} ×\mathrm{4}! \\ $$$${or} \\ $$$${C}_{\mathrm{2}} ^{\mathrm{6}} ×\mathrm{2}×{P}_{\mathrm{4}} ^{\mathrm{8}} \\ $$
