
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 113368 by mr W last updated on 12/Sep/20

$$\mathrm{There}\:\mathrm{are}\:\mathrm{4}\:\mathrm{identical}\:\mathrm{mathematics} \\ $$$$\mathrm{books},\:\mathrm{3}\:\mathrm{identical}\:\mathrm{physics}\:\mathrm{books},\:\mathrm{2} \\ $$$$\mathrm{identical}\:\mathrm{chemistry}\:\mathrm{books}. \\ $$$$\mathrm{in}\:\mathrm{how}\:\mathrm{many}\:\mathrm{ways}\:\:\mathrm{can}\:\mathrm{you}\:\mathrm{compile} \\ $$$$\mathrm{the}\:\mathrm{9}\:\mathrm{books}\:\mathrm{such}\:\mathrm{that}\:\mathrm{same}\:\mathrm{books}\:\mathrm{are} \\ $$$$\mathrm{not}\:\mathrm{mutually}\:\mathrm{adjacent}. \\ $$
Answered by mr W last updated on 15/Sep/20
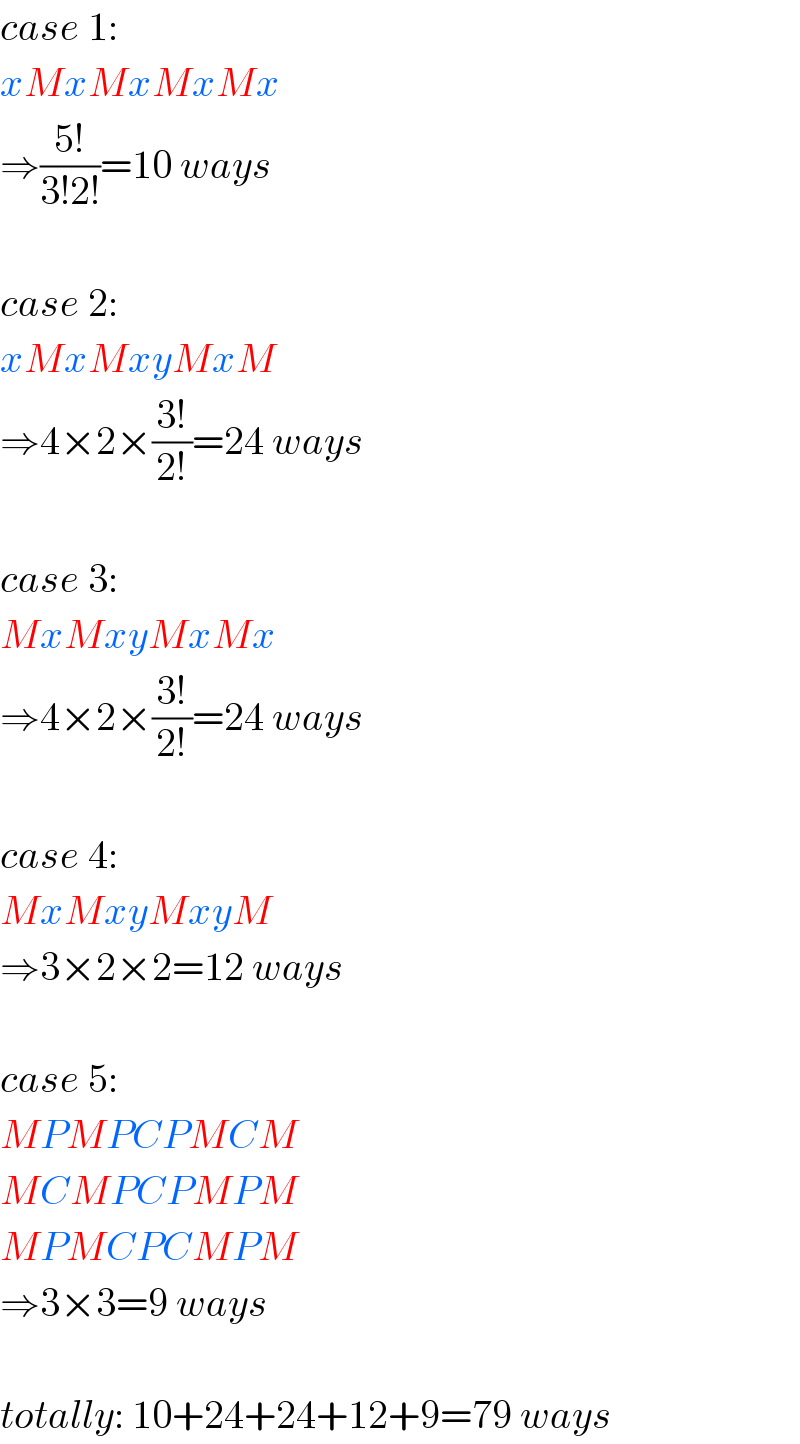
$${case}\:\mathrm{1}: \\ $$$${xMxMxMxMx} \\ $$$$\Rightarrow\frac{\mathrm{5}!}{\mathrm{3}!\mathrm{2}!}=\mathrm{10}\:{ways} \\ $$$$ \\ $$$${case}\:\mathrm{2}: \\ $$$${xMxMxyMxM} \\ $$$$\Rightarrow\mathrm{4}×\mathrm{2}×\frac{\mathrm{3}!}{\mathrm{2}!}=\mathrm{24}\:{ways} \\ $$$$ \\ $$$${case}\:\mathrm{3}: \\ $$$${MxMxyMxMx} \\ $$$$\Rightarrow\mathrm{4}×\mathrm{2}×\frac{\mathrm{3}!}{\mathrm{2}!}=\mathrm{24}\:{ways} \\ $$$$ \\ $$$${case}\:\mathrm{4}: \\ $$$${MxMxyMxyM} \\ $$$$\Rightarrow\mathrm{3}×\mathrm{2}×\mathrm{2}=\mathrm{12}\:{ways} \\ $$$$ \\ $$$${case}\:\mathrm{5}: \\ $$$${MPMPCPMCM} \\ $$$${MCMPCPMPM} \\ $$$${MPMCPCMPM} \\ $$$$\Rightarrow\mathrm{3}×\mathrm{3}=\mathrm{9}\:{ways} \\ $$$$ \\ $$$${totally}:\:\mathrm{10}+\mathrm{24}+\mathrm{24}+\mathrm{12}+\mathrm{9}=\mathrm{79}\:{ways} \\ $$
