Question and Answers Forum

All Questions      Topic List

UNKNOWN Questions

Previous in All Question      Next in All Question      

Previous in UNKNOWN      Next in UNKNOWN      

Question Number 27295 by iy last updated on 04/Jan/18

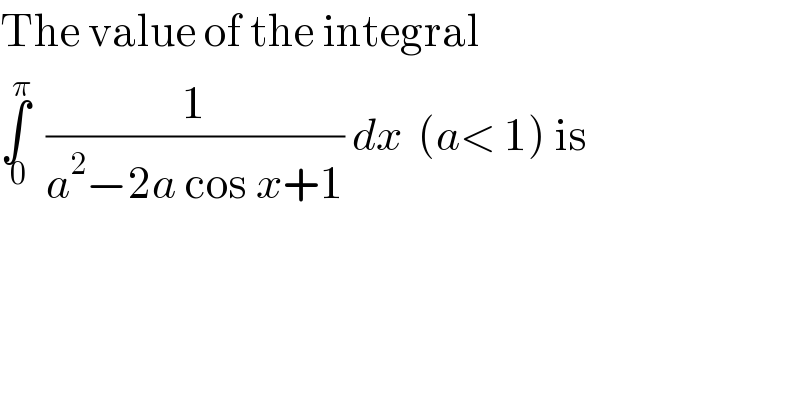
The value of the integral ∫_( 0) ^π (1/(a^2 −2a cos x+1)) dx (a< 1) is

$$\mathrm{The}\:\mathrm{value}\:\mathrm{of}\:\mathrm{the}\:\mathrm{integral} \\ $$$$\underset{\:\mathrm{0}} {\overset{\pi} {\int}}\:\:\frac{\mathrm{1}}{{a}^{\mathrm{2}} −\mathrm{2}{a}\:\mathrm{cos}\:{x}+\mathrm{1}}\:{dx}\:\:\left({a}<\:\mathrm{1}\right)\:\mathrm{is} \\ $$

Commented by abdo imad last updated on 04/Jan/18

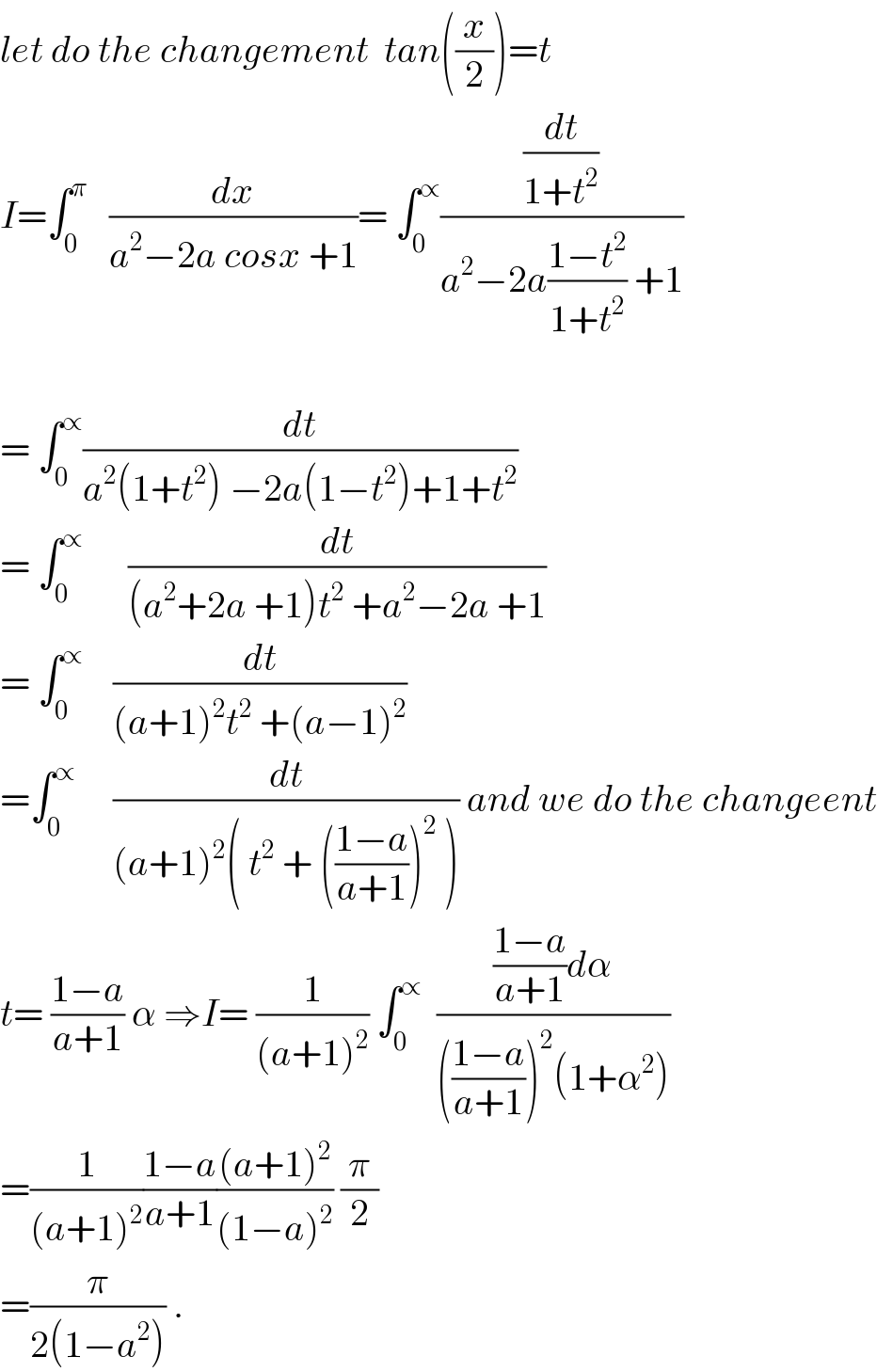
let do the changement tan((x/2))=t I=∫_0 ^π (dx/(a^2 −2a cosx +1))= ∫_0 ^∝ ((dt/(1+t^2 ))/(a^2 −2a((1−t^2 )/(1+t^2 )) +1)) = ∫_0 ^∝ (dt/(a^2 (1+t^2 ) −2a(1−t^2 )+1+t^2 )) = ∫_0 ^∝ (dt/((a^2 +2a +1)t^2 +a^2 −2a +1)) = ∫_0 ^∝ (dt/((a+1)^2 t^2 +(a−1)^2 )) =∫_0 ^∝ (dt/((a+1)^2 ( t^2 + (((1−a)/(a+1)))^2 ))) and we do the changeent t= ((1−a)/(a+1)) α ⇒I= (1/((a+1)^2 )) ∫_0 ^∝ ((((1−a)/(a+1))dα)/((((1−a)/(a+1)))^2 (1+α^2 ))) =(1/((a+1)^2 ))((1−a)/(a+1))(((a+1)^2 )/((1−a)^2 )) (π/2) =(π/(2(1−a^2 ))) .

$${let}\:{do}\:{the}\:{changement}\:\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t} \\ $$$${I}=\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{dx}}{{a}^{\mathrm{2}} −\mathrm{2}{a}\:{cosx}\:+\mathrm{1}}=\:\int_{\mathrm{0}} ^{\propto} \frac{\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }}{{a}^{\mathrm{2}} −\mathrm{2}{a}\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\:+\mathrm{1}} \\ $$$$ \\ $$$$=\:\int_{\mathrm{0}} ^{\propto} \frac{{dt}}{{a}^{\mathrm{2}} \left(\mathrm{1}+{t}^{\mathrm{2}} \right)\:−\mathrm{2}{a}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)+\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\:\int_{\mathrm{0}} ^{\propto} \:\:\:\:\:\:\frac{{dt}}{\left({a}^{\mathrm{2}} +\mathrm{2}{a}\:+\mathrm{1}\right){t}^{\mathrm{2}} \:+{a}^{\mathrm{2}} −\mathrm{2}{a}\:+\mathrm{1}} \\ $$$$=\:\int_{\mathrm{0}} ^{\propto} \:\:\:\:\frac{{dt}}{\left({a}+\mathrm{1}\right)^{\mathrm{2}} {t}^{\mathrm{2}} \:+\left({a}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{0}} ^{\propto} \:\:\:\:\:\frac{{dt}}{\left({a}+\mathrm{1}\right)^{\mathrm{2}} \left(\:{t}^{\mathrm{2}} \:+\:\left(\frac{\mathrm{1}−{a}}{{a}+\mathrm{1}}\right)^{\mathrm{2}} \:\right)}\:{and}\:{we}\:{do}\:{the}\:{changeent} \\ $$$${t}=\:\frac{\mathrm{1}−{a}}{{a}+\mathrm{1}}\:\alpha\:\Rightarrow{I}=\:\frac{\mathrm{1}}{\left({a}+\mathrm{1}\right)^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\propto} \:\:\frac{\frac{\mathrm{1}−{a}}{{a}+\mathrm{1}}{d}\alpha}{\left(\frac{\mathrm{1}−{a}}{{a}+\mathrm{1}}\right)^{\mathrm{2}} \left(\mathrm{1}+\alpha^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{1}}{\left({a}+\mathrm{1}\right)^{\mathrm{2}} }\frac{\mathrm{1}−{a}}{{a}+\mathrm{1}}\frac{\left({a}+\mathrm{1}\right)^{\mathrm{2}} }{\left(\mathrm{1}−{a}\right)^{\mathrm{2}} }\:\frac{\pi}{\mathrm{2}} \\ $$$$=\frac{\pi}{\mathrm{2}\left(\mathrm{1}−{a}^{\mathrm{2}} \right)}\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com