
Question Number 153916 by EDWIN88 last updated on 12/Sep/21
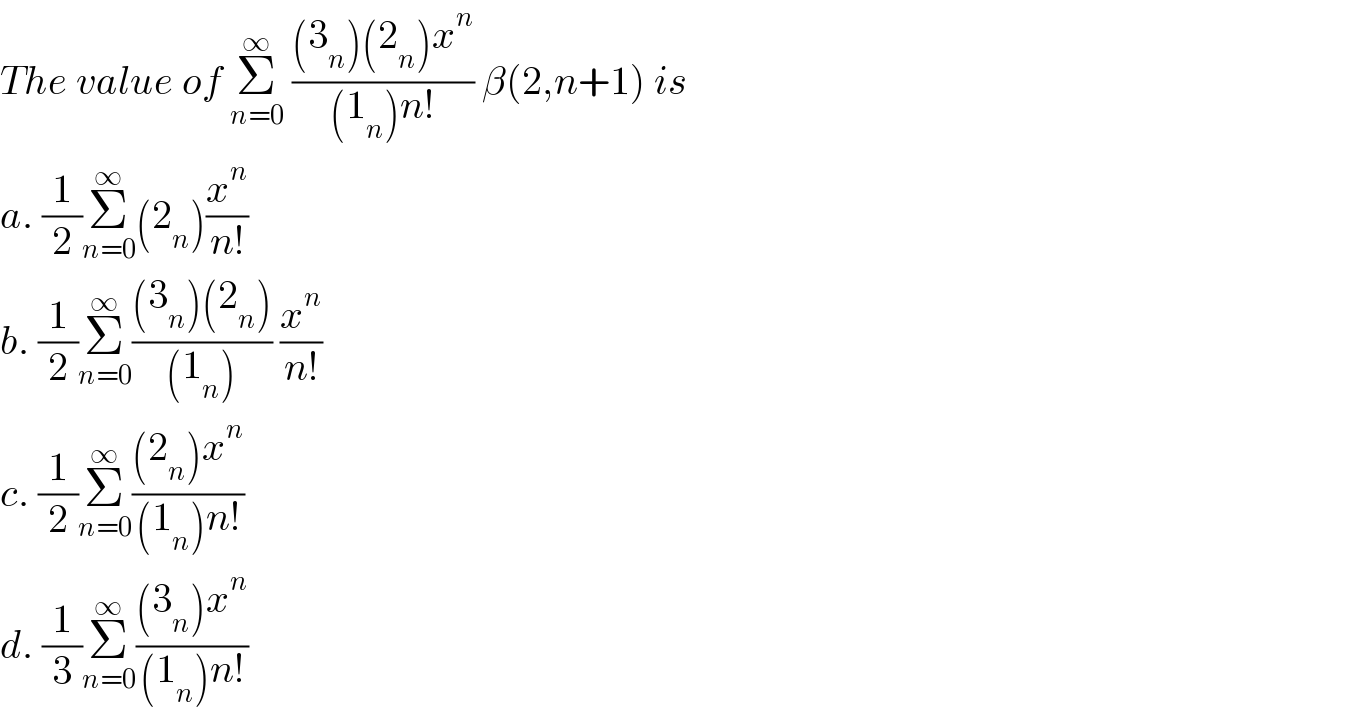
$${The}\:{value}\:{of}\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\left(\mathrm{3}_{{n}} \right)\left(\mathrm{2}_{{n}} \right){x}^{{n}} }{\left(\mathrm{1}_{{n}} \right){n}!}\:\beta\left(\mathrm{2},{n}+\mathrm{1}\right)\:{is} \\ $$$${a}.\:\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\mathrm{2}_{{n}} \right)\frac{{x}^{{n}} }{{n}!} \\ $$$${b}.\:\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{3}_{{n}} \right)\left(\mathrm{2}_{{n}} \right)}{\left(\mathrm{1}_{{n}} \right)}\:\frac{{x}^{{n}} }{{n}!} \\ $$$${c}.\:\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{2}_{{n}} \right){x}^{{n}} }{\left(\mathrm{1}_{{n}} \right){n}!} \\ $$$${d}.\:\frac{\mathrm{1}}{\mathrm{3}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{3}_{{n}} \right){x}^{{n}} }{\left(\mathrm{1}_{{n}} \right){n}!} \\ $$
