
Question Number 113986 by deepraj123 last updated on 16/Sep/20
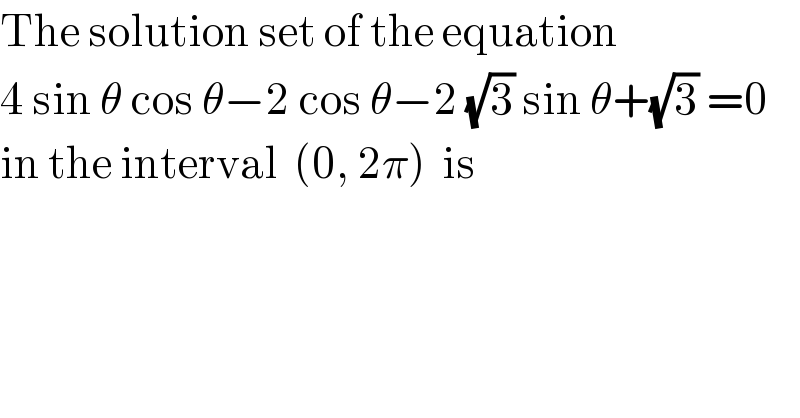
$$\mathrm{The}\:\mathrm{solution}\:\mathrm{set}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{4}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta−\mathrm{2}\:\mathrm{cos}\:\theta−\mathrm{2}\:\sqrt{\mathrm{3}}\:\mathrm{sin}\:\theta+\sqrt{\mathrm{3}}\:=\mathrm{0} \\ $$$$\mathrm{in}\:\mathrm{the}\:\mathrm{interval}\:\:\left(\mathrm{0},\:\mathrm{2}\pi\right)\:\:\mathrm{is} \\ $$
Answered by MJS_new last updated on 16/Sep/20
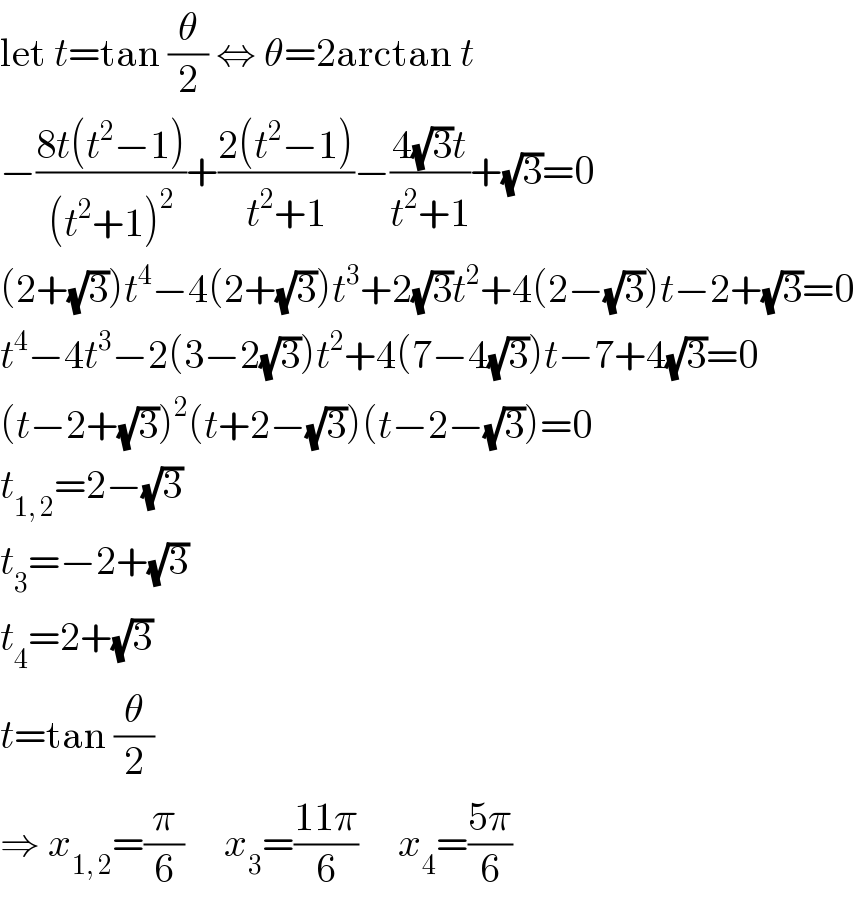
$$\mathrm{let}\:{t}=\mathrm{tan}\:\frac{\theta}{\mathrm{2}}\:\Leftrightarrow\:\theta=\mathrm{2arctan}\:{t} \\ $$$$−\frac{\mathrm{8}{t}\left({t}^{\mathrm{2}} −\mathrm{1}\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{2}\left({t}^{\mathrm{2}} −\mathrm{1}\right)}{{t}^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{4}\sqrt{\mathrm{3}}{t}}{{t}^{\mathrm{2}} +\mathrm{1}}+\sqrt{\mathrm{3}}=\mathrm{0} \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{3}}\right){t}^{\mathrm{4}} −\mathrm{4}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right){t}^{\mathrm{3}} +\mathrm{2}\sqrt{\mathrm{3}}{t}^{\mathrm{2}} +\mathrm{4}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right){t}−\mathrm{2}+\sqrt{\mathrm{3}}=\mathrm{0} \\ $$$${t}^{\mathrm{4}} −\mathrm{4}{t}^{\mathrm{3}} −\mathrm{2}\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{3}}\right){t}^{\mathrm{2}} +\mathrm{4}\left(\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\right){t}−\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}=\mathrm{0} \\ $$$$\left({t}−\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \left({t}+\mathrm{2}−\sqrt{\mathrm{3}}\right)\left({t}−\mathrm{2}−\sqrt{\mathrm{3}}\right)=\mathrm{0} \\ $$$${t}_{\mathrm{1},\:\mathrm{2}} =\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$${t}_{\mathrm{3}} =−\mathrm{2}+\sqrt{\mathrm{3}} \\ $$$${t}_{\mathrm{4}} =\mathrm{2}+\sqrt{\mathrm{3}} \\ $$$${t}=\mathrm{tan}\:\frac{\theta}{\mathrm{2}} \\ $$$$\Rightarrow\:{x}_{\mathrm{1},\:\mathrm{2}} =\frac{\pi}{\mathrm{6}}\:\:\:\:\:{x}_{\mathrm{3}} =\frac{\mathrm{11}\pi}{\mathrm{6}}\:\:\:\:\:{x}_{\mathrm{4}} =\frac{\mathrm{5}\pi}{\mathrm{6}} \\ $$
