Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 42299 by Rio Michael last updated on 22/Aug/18

The set X and Y have five elementseach . Given that ΣX=25,ΣY=55,ΣX^2 =165 and ΣY^2 =765 and a linear Function y= px + q tranforms the set X into the set Y,where p and q are positive constants. a) Find the mean and Variance of X and Y hence,or otherwise , b)find the values of p and q.

$${The}\:{set}\:{X}\:{and}\:{Y}\:{have}\:{five}\:{elementseach}\:. \\ $$$${Given}\:{that}\:\Sigma{X}=\mathrm{25},\Sigma{Y}=\mathrm{55},\Sigma{X}^{\mathrm{2}} =\mathrm{165}\:{and}\:\Sigma{Y}^{\mathrm{2}} =\mathrm{765} \\ $$$${and}\:{a}\:{linear}\:{Function}\:{y}=\:{px}\:+\:{q}\:\:{tranforms}\:{the}\:{set}\:{X}\:{into}\:{the}\:{set}\: \\ $$$${Y},{where}\:{p}\:{and}\:{q}\:{are}\:{positive}\:{constants}. \\ $$$$\left.{a}\right)\:{Find}\:{the}\:{mean}\:{and}\:{Variance}\:{of}\:{X}\:{and}\:{Y} \\ $$$${hence},{or}\:{otherwise}\:, \\ $$$$\left.{b}\right){find}\:{the}\:{values}\:{of}\:{p}\:{and}\:{q}. \\ $$

Answered by MJS last updated on 22/Aug/18

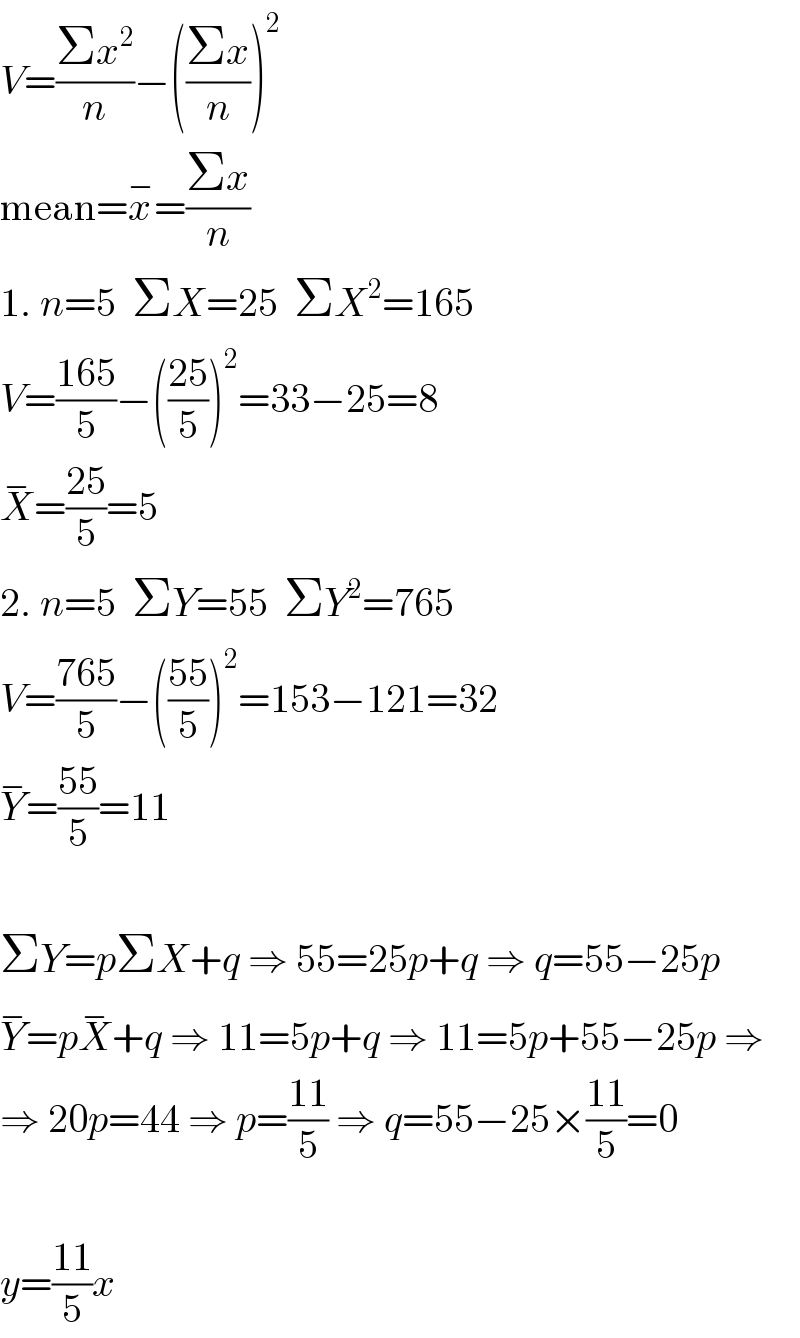
V=((Σx^2 )/n)−(((Σx)/n))^2 mean=x^− =((Σx)/n) 1. n=5 ΣX=25 ΣX^2 =165 V=((165)/5)−(((25)/5))^2 =33−25=8 X^− =((25)/5)=5 2. n=5 ΣY=55 ΣY^2 =765 V=((765)/5)−(((55)/5))^2 =153−121=32 Y^− =((55)/5)=11 ΣY=pΣX+q ⇒ 55=25p+q ⇒ q=55−25p Y^− =pX^− +q ⇒ 11=5p+q ⇒ 11=5p+55−25p ⇒ ⇒ 20p=44 ⇒ p=((11)/5) ⇒ q=55−25×((11)/5)=0 y=((11)/5)x

$${V}=\frac{\Sigma{x}^{\mathrm{2}} }{{n}}−\left(\frac{\Sigma{x}}{{n}}\right)^{\mathrm{2}} \\ $$$$\mathrm{mean}=\overset{−} {{x}}=\frac{\Sigma{x}}{{n}} \\ $$$$\mathrm{1}.\:{n}=\mathrm{5}\:\:\Sigma{X}=\mathrm{25}\:\:\Sigma{X}^{\mathrm{2}} =\mathrm{165} \\ $$$${V}=\frac{\mathrm{165}}{\mathrm{5}}−\left(\frac{\mathrm{25}}{\mathrm{5}}\right)^{\mathrm{2}} =\mathrm{33}−\mathrm{25}=\mathrm{8} \\ $$$$\overset{−} {{X}}=\frac{\mathrm{25}}{\mathrm{5}}=\mathrm{5} \\ $$$$\mathrm{2}.\:{n}=\mathrm{5}\:\:\Sigma{Y}=\mathrm{55}\:\:\Sigma{Y}^{\mathrm{2}} =\mathrm{765} \\ $$$${V}=\frac{\mathrm{765}}{\mathrm{5}}−\left(\frac{\mathrm{55}}{\mathrm{5}}\right)^{\mathrm{2}} =\mathrm{153}−\mathrm{121}=\mathrm{32} \\ $$$$\overset{−} {{Y}}=\frac{\mathrm{55}}{\mathrm{5}}=\mathrm{11} \\ $$$$ \\ $$$$\Sigma{Y}={p}\Sigma{X}+{q}\:\Rightarrow\:\mathrm{55}=\mathrm{25}{p}+{q}\:\Rightarrow\:{q}=\mathrm{55}−\mathrm{25}{p} \\ $$$$\overset{−} {{Y}}={p}\overset{−} {{X}}+{q}\:\Rightarrow\:\mathrm{11}=\mathrm{5}{p}+{q}\:\Rightarrow\:\mathrm{11}=\mathrm{5}{p}+\mathrm{55}−\mathrm{25}{p}\:\Rightarrow \\ $$$$\Rightarrow\:\mathrm{20}{p}=\mathrm{44}\:\Rightarrow\:{p}=\frac{\mathrm{11}}{\mathrm{5}}\:\Rightarrow\:{q}=\mathrm{55}−\mathrm{25}×\frac{\mathrm{11}}{\mathrm{5}}=\mathrm{0} \\ $$$$ \\ $$$${y}=\frac{\mathrm{11}}{\mathrm{5}}{x} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com