Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 145443 by 7770 last updated on 04/Jul/21

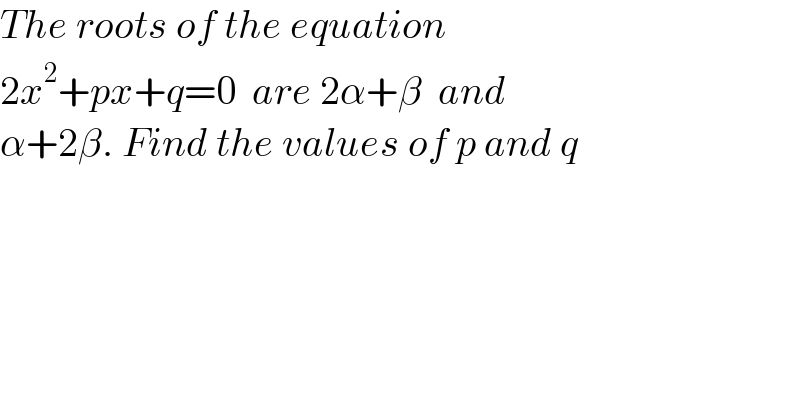
The roots of the equation 2x^2 +px+q=0 are 2α+β and α+2β. Find the values of p and q

$${The}\:{roots}\:{of}\:{the}\:{equation} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +{px}+{q}=\mathrm{0}\:\:{are}\:\mathrm{2}\alpha+\beta\:\:{and} \\ $$$$\alpha+\mathrm{2}\beta.\:{Find}\:{the}\:{values}\:{of}\:{p}\:{and}\:{q} \\ $$

Answered by Olaf_Thorendsen last updated on 05/Jul/21

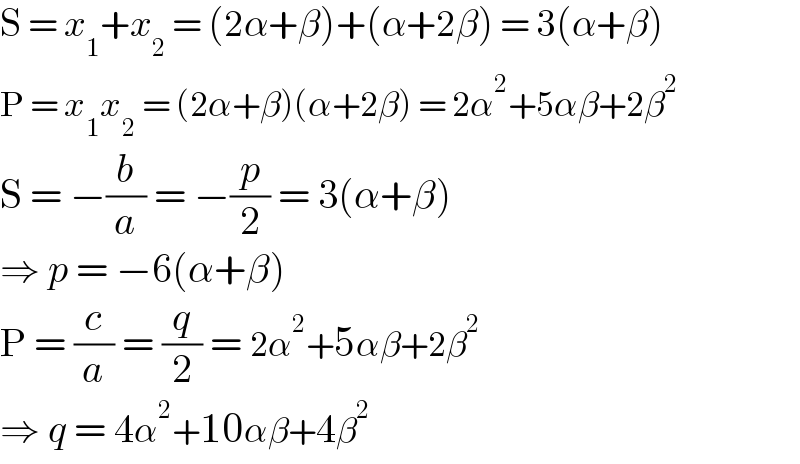
S = x_1 +x_2 = (2α+β)+(α+2β) = 3(α+β) P = x_1 x_2 = (2α+β)(α+2β) = 2α^2 +5αβ+2β^2 S = −(b/a) = −(p/2) = 3(α+β) ⇒ p = −6(α+β) P = (c/a) = (q/2) = 2α^2 +5αβ+2β^2 ⇒ q = 4α^2 +10αβ+4β^2

$$\mathrm{S}\:=\:{x}_{\mathrm{1}} +{x}_{\mathrm{2}} \:=\:\left(\mathrm{2}\alpha+\beta\right)+\left(\alpha+\mathrm{2}\beta\right)\:=\:\mathrm{3}\left(\alpha+\beta\right) \\ $$$$\mathrm{P}\:=\:{x}_{\mathrm{1}} {x}_{\mathrm{2}} \:=\:\left(\mathrm{2}\alpha+\beta\right)\left(\alpha+\mathrm{2}\beta\right)\:=\:\mathrm{2}\alpha^{\mathrm{2}} +\mathrm{5}\alpha\beta+\mathrm{2}\beta^{\mathrm{2}} \\ $$$$\mathrm{S}\:=\:−\frac{{b}}{{a}}\:=\:−\frac{{p}}{\mathrm{2}}\:=\:\mathrm{3}\left(\alpha+\beta\right) \\ $$$$\Rightarrow\:{p}\:=\:−\mathrm{6}\left(\alpha+\beta\right) \\ $$$$\mathrm{P}\:=\:\frac{{c}}{{a}}\:=\:\frac{{q}}{\mathrm{2}}\:=\:\mathrm{2}\alpha^{\mathrm{2}} +\mathrm{5}\alpha\beta+\mathrm{2}\beta^{\mathrm{2}} \\ $$$$\Rightarrow\:{q}\:=\:\mathrm{4}\alpha^{\mathrm{2}} +\mathrm{10}\alpha\beta+\mathrm{4}\beta^{\mathrm{2}} \\ $$

Answered by Rasheed.Sindhi last updated on 05/Jul/21

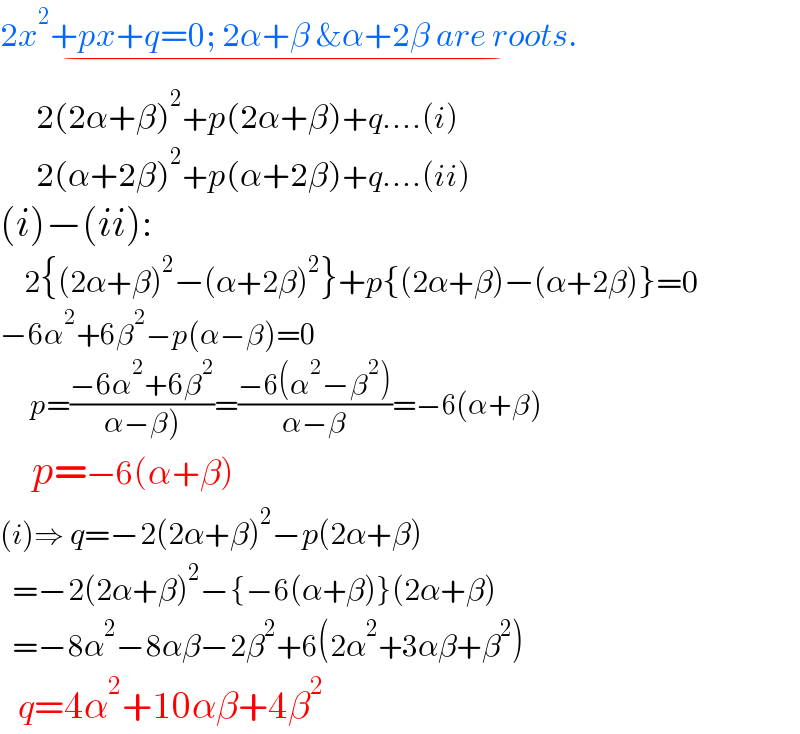
2x^2 +px+q=0; 2α+β &α+2β are roots._(−) 2(2α+β)^2 +p(2α+β)+q....(i) 2(α+2β)^2 +p(α+2β)+q....(ii) (i)−(ii): 2{(2α+β)^2 −(α+2β)^2 }+p{(2α+β)−(α+2β)}=0 −6α^2 +6β^2 −p(α−β)=0 p=((−6α^2 +6β^2 )/(α−β)))=((−6(α^2 −β^2 ))/(α−β))=−6(α+β) p=−6(α+β) (i)⇒ q=−2(2α+β)^2 −p(2α+β) =−2(2α+β)^2 −{−6(α+β)}(2α+β) =−8α^2 −8αβ−2β^2 +6(2α^2 +3αβ+β^2 ) q=4α^2 +10αβ+4β^2

$$\underset{−} {\mathrm{2}{x}^{\mathrm{2}} +{px}+{q}=\mathrm{0};\:\mathrm{2}\alpha+\beta\:\&\alpha+\mathrm{2}\beta\:{are}\:{roots}.} \\ $$$$\:\:\:\:\:\:\mathrm{2}\left(\mathrm{2}\alpha+\beta\right)^{\mathrm{2}} +{p}\left(\mathrm{2}\alpha+\beta\right)+{q}....\left({i}\right) \\ $$$$\:\:\:\:\:\:\mathrm{2}\left(\alpha+\mathrm{2}\beta\right)^{\mathrm{2}} +{p}\left(\alpha+\mathrm{2}\beta\right)+{q}....\left({ii}\right) \\ $$$$\left({i}\right)−\left({ii}\right): \\ $$$$\:\:\:\:\mathrm{2}\left\{\left(\mathrm{2}\alpha+\beta\right)^{\mathrm{2}} −\left(\alpha+\mathrm{2}\beta\right)^{\mathrm{2}} \right\}+{p}\left\{\left(\mathrm{2}\alpha+\beta\right)−\left(\alpha+\mathrm{2}\beta\right)\right\}=\mathrm{0} \\ $$$$−\mathrm{6}\alpha^{\mathrm{2}} +\mathrm{6}\beta^{\mathrm{2}} −{p}\left(\alpha−\beta\right)=\mathrm{0} \\ $$$$\:\:\:\:\:{p}=\frac{−\mathrm{6}\alpha^{\mathrm{2}} +\mathrm{6}\beta^{\mathrm{2}} }{\left.\alpha−\beta\right)}=\frac{−\mathrm{6}\left(\alpha^{\mathrm{2}} −\beta^{\mathrm{2}} \right)}{\alpha−\beta}=−\mathrm{6}\left(\alpha+\beta\right) \\ $$$$\:\:\:\:{p}=−\mathrm{6}\left(\alpha+\beta\right) \\ $$$$\left({i}\right)\Rightarrow\:{q}=−\mathrm{2}\left(\mathrm{2}\alpha+\beta\right)^{\mathrm{2}} −{p}\left(\mathrm{2}\alpha+\beta\right) \\ $$$$\:\:=−\mathrm{2}\left(\mathrm{2}\alpha+\beta\right)^{\mathrm{2}} −\left\{−\mathrm{6}\left(\alpha+\beta\right)\right\}\left(\mathrm{2}\alpha+\beta\right) \\ $$$$\:\:=−\mathrm{8}\alpha^{\mathrm{2}} −\mathrm{8}\alpha\beta−\mathrm{2}\beta^{\mathrm{2}} +\mathrm{6}\left(\mathrm{2}\alpha^{\mathrm{2}} +\mathrm{3}\alpha\beta+\beta^{\mathrm{2}} \right) \\ $$$$\:\:\:{q}=\mathrm{4}\alpha^{\mathrm{2}} +\mathrm{10}\alpha\beta+\mathrm{4}\beta^{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com