
Question Number 217058 by ArshadS last updated on 28/Feb/25

$$\mathrm{The}\:\mathrm{quadratic}\:\mathrm{equation}\:\:\mathrm{has}\:\mathrm{two}\:\mathrm{equal}\:\mathrm{roots}: \\ $$$$\:\:\:\:\:{x}^{\mathrm{2}} +\left({k}−\mathrm{3}\right){x}+{k}=\mathrm{0} \\ $$$$\left(\mathrm{a}\right)\:\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\:{k}. \\ $$$$\left(\mathrm{b}\right)\:\mathrm{For}\:\mathrm{this}\:\mathrm{value}\:\mathrm{of}\:\:{k},\:\mathrm{solve}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{for}\:{x} \\ $$$$\left(\mathrm{c}\right)\mathrm{If}\:\:{x}\:\mathrm{is}\:\mathrm{the}\:\mathrm{length}\:\mathrm{of}\:\mathrm{a}\:\mathrm{rectangle}\:\mathrm{and}\:\mathrm{its}\:\mathrm{width}\:\mathrm{is}\:{x}−\mathrm{2},\:\:\mathrm{find}\:\mathrm{the}\:\mathrm{area}\: \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{rectangle}. \\ $$
Answered by Rasheed.Sindhi last updated on 28/Feb/25
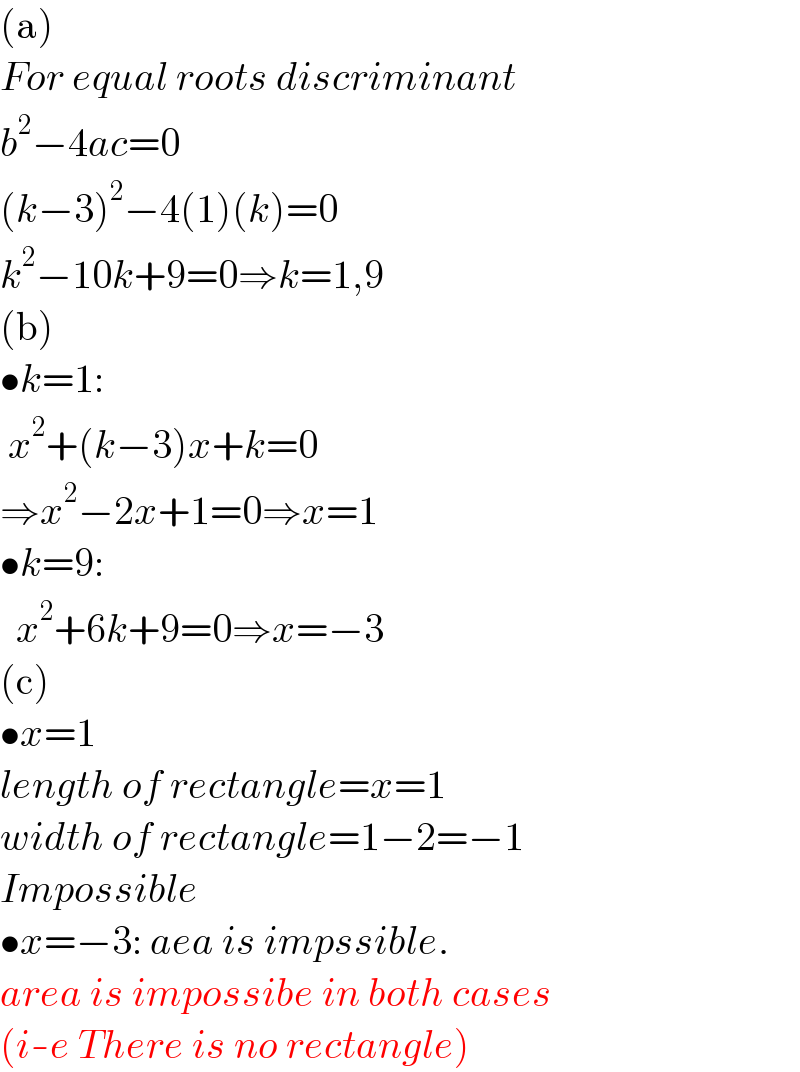
$$\left(\mathrm{a}\right) \\ $$$${For}\:{equal}\:{roots}\:{discriminant} \\ $$$${b}^{\mathrm{2}} −\mathrm{4}{ac}=\mathrm{0} \\ $$$$\left({k}−\mathrm{3}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}\right)\left({k}\right)=\mathrm{0} \\ $$$${k}^{\mathrm{2}} −\mathrm{10}{k}+\mathrm{9}=\mathrm{0}\Rightarrow{k}=\mathrm{1},\mathrm{9} \\ $$$$\left(\mathrm{b}\right) \\ $$$$\bullet{k}=\mathrm{1}: \\ $$$$\:{x}^{\mathrm{2}} +\left({k}−\mathrm{3}\right){x}+{k}=\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}=\mathrm{0}\Rightarrow{x}=\mathrm{1} \\ $$$$\bullet{k}=\mathrm{9}: \\ $$$$\:\:{x}^{\mathrm{2}} +\mathrm{6}{k}+\mathrm{9}=\mathrm{0}\Rightarrow{x}=−\mathrm{3} \\ $$$$\left(\mathrm{c}\right) \\ $$$$\bullet{x}=\mathrm{1} \\ $$$${length}\:{of}\:{rectangle}={x}=\mathrm{1} \\ $$$${width}\:{of}\:{rectangle}=\mathrm{1}−\mathrm{2}=−\mathrm{1} \\ $$$${Impossible} \\ $$$$\bullet{x}=−\mathrm{3}:\:{aea}\:{is}\:{impssible}. \\ $$$${area}\:{is}\:{impossibe}\:{in}\:{both}\:{cases} \\ $$$$\left({i}-{e}\:{There}\:{is}\:{no}\:{rectangle}\right) \\ $$
