
Question Number 18322 by Tinkutara last updated on 18/Jul/17

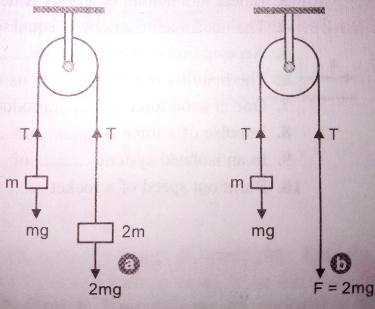
$$\mathrm{The}\:\mathrm{pulley}\:\mathrm{arrangements}\:\mathrm{are}\:\mathrm{identical}. \\ $$$$\mathrm{The}\:\mathrm{mass}\:\mathrm{of}\:\mathrm{the}\:\mathrm{rope}\:\mathrm{is}\:\mathrm{negligible}.\:\mathrm{In} \\ $$$$\left(\mathrm{a}\right),\:\mathrm{the}\:\mathrm{mass}\:{m}\:\mathrm{is}\:\mathrm{lifted}\:\mathrm{up}\:\mathrm{by}\:\mathrm{attaching} \\ $$$$\mathrm{a}\:\mathrm{mass}\:\left(\mathrm{2}{m}\right)\:\mathrm{to}\:\mathrm{the}\:\mathrm{other}\:\mathrm{end}\:\mathrm{of}\:\mathrm{the}\:\mathrm{rope}. \\ $$$$\mathrm{In}\:\left(\mathrm{b}\right),\:{m}\:\mathrm{is}\:\mathrm{lifted}\:\mathrm{up}\:\mathrm{by}\:\mathrm{pulling}\:\mathrm{the} \\ $$$$\mathrm{other}\:\mathrm{end}\:\mathrm{of}\:\mathrm{the}\:\mathrm{rope}\:\mathrm{with}\:\mathrm{a}\:\mathrm{constant} \\ $$$$\mathrm{downward}\:\mathrm{force}\:{F}\:=\:\mathrm{2}{mg}.\:\mathrm{In}\:\mathrm{which} \\ $$$$\mathrm{case},\:\mathrm{the}\:\mathrm{acceleration}\:\mathrm{of}\:{m}\:\mathrm{is}\:\mathrm{more}? \\ $$
Commented by Tinkutara last updated on 18/Jul/17
Answered by ajfour last updated on 18/Jul/17

$$\mathrm{In}\:\left(\mathrm{b}\right)\:\mathrm{Tension}\:\mathrm{in}\:\mathrm{rope},\:\mathrm{T}_{\mathrm{b}} =\mathrm{2mg} \\ $$$$\mathrm{T}_{\mathrm{b}} −\mathrm{mg}=\mathrm{ma}_{\mathrm{b}} \\ $$$$\mathrm{2mg}−\mathrm{mg}=\mathrm{ma}_{\mathrm{b}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{a}_{\mathrm{b}} \:=\mathrm{g} \\ $$$$\mathrm{In}\:\left(\mathrm{a}\right)\:\mathrm{2mg}−\mathrm{T}_{\mathrm{a}} =\mathrm{2ma}_{\mathrm{a}} \\ $$$$\mathrm{and}\:\:\:\:\:\:\mathrm{T}_{\mathrm{a}} −\mathrm{mg}=\mathrm{ma}_{\mathrm{a}} \\ $$$$\mathrm{adding}:\:\:\:\:\:\:\:\mathrm{mg}=\mathrm{3ma}_{\mathrm{a}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{a}_{\mathrm{a}} \:=\frac{\mathrm{g}}{\mathrm{3}}\:. \\ $$$$\:\:\:\:\:\:\mathrm{a}_{\mathrm{b}} \:>\:\mathrm{a}_{\mathrm{a}} \:. \\ $$
Commented by Tinkutara last updated on 19/Jul/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
