
Question Number 172099 by Mastermind last updated on 23/Jun/22

$${The}\:{probability}\:{that}\:{Abiola}\:{will}\:{be} \\ $$$${late}\:{to}\:{office}\:{on}\:{a}\:{given}\:{day}\:{is}\frac{\mathrm{2}}{\mathrm{5}}\:.\:{in} \\ $$$${a}\:{given}\:{week}\:{of}\:{six}\:{days},\:{find}\:{the}\: \\ $$$$\left.\mathrm{1}\right)\:{probability}\:{that}\:{he}\:{will}\:{be}\:{late}\:{of} \\ $$$${only}\:\mathrm{3}\:{days} \\ $$$$\left.\mathrm{2}\right)\:{not}\:{be}\:{late}\:{in}\:{the}\:{week} \\ $$
Answered by mr W last updated on 24/Jun/22
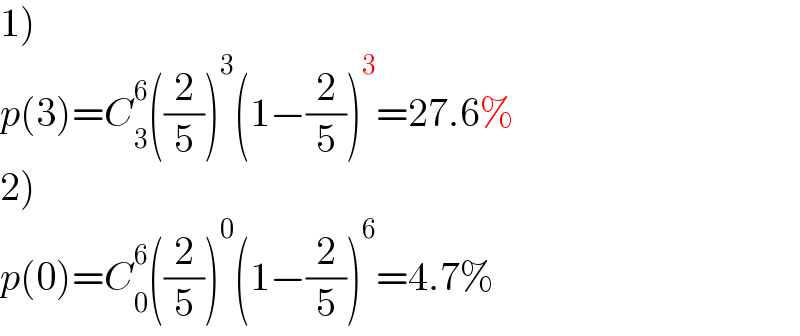
$$\left.\mathrm{1}\right) \\ $$$${p}\left(\mathrm{3}\right)={C}_{\mathrm{3}} ^{\mathrm{6}} \left(\frac{\mathrm{2}}{\mathrm{5}}\right)^{\mathrm{3}} \left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{5}}\right)^{\mathrm{3}} =\mathrm{27}.\mathrm{6\%} \\ $$$$\left.\mathrm{2}\right) \\ $$$${p}\left(\mathrm{0}\right)={C}_{\mathrm{0}} ^{\mathrm{6}} \left(\frac{\mathrm{2}}{\mathrm{5}}\right)^{\mathrm{0}} \left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{5}}\right)^{\mathrm{6}} =\mathrm{4}.\mathrm{7\%} \\ $$
