Question Number 191149 by SLVR last updated on 19/Apr/23
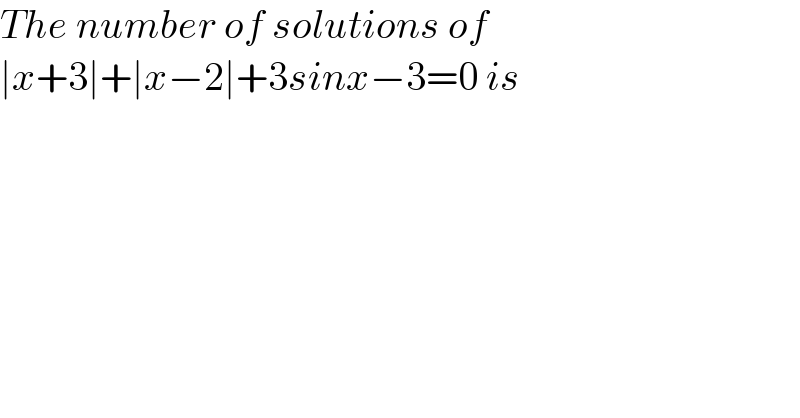
$${The}\:{number}\:{of}\:{solutions}\:{of} \\ $$$$\mid{x}+\mathrm{3}\mid+\mid{x}−\mathrm{2}\mid+\mathrm{3}{sinx}−\mathrm{3}=\mathrm{0}\:{is} \\ $$
Commented by SLVR last updated on 19/Apr/23
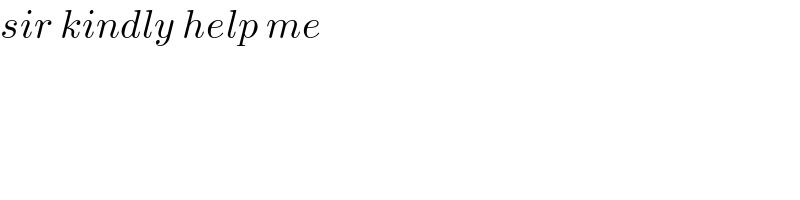
$${sir}\:{kindly}\:{help}\:{me}\: \\ $$
Commented by SLVR last updated on 19/Apr/23
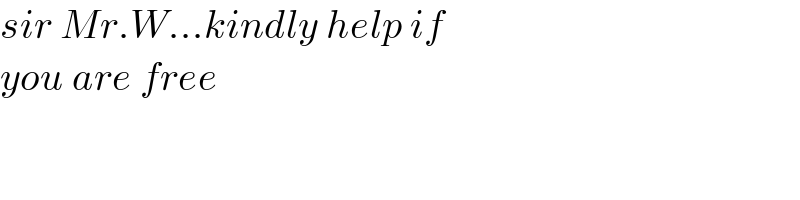
$${sir}\:{Mr}.{W}...{kindly}\:{help}\:{if} \\ $$$${you}\:{are}\:{free} \\ $$
Commented by Frix last updated on 19/Apr/23
I'm Freex ��
Answered by Frix last updated on 19/Apr/23
![∣x+3∣+∣x−2∣=3(1−sin x) f_1 (x)=∣x+3∣+∣x−2∣= { ((−2x−1; x<−3)),((5; −3≤x≤2)),((2x+1; x>2)) :} 0≤(f_2 (x)=3(1−sin x))≤6 x∈[−(7/2); (5/2)]: 5≤f_1 (x)≤6 ⇒ Solutions possible within this interval ⇒ 2 solutions: x_1 =−π+sin^(−1) (2/3) x_2 =−sin^(−1) (2/3)](Q191156.png)
$$\mid{x}+\mathrm{3}\mid+\mid{x}−\mathrm{2}\mid=\mathrm{3}\left(\mathrm{1}−\mathrm{sin}\:{x}\right) \\ $$$${f}_{\mathrm{1}} \left({x}\right)=\mid{x}+\mathrm{3}\mid+\mid{x}−\mathrm{2}\mid=\begin{cases}{−\mathrm{2}{x}−\mathrm{1};\:{x}<−\mathrm{3}}\\{\mathrm{5};\:−\mathrm{3}\leqslant{x}\leqslant\mathrm{2}}\\{\mathrm{2}{x}+\mathrm{1};\:{x}>\mathrm{2}}\end{cases} \\ $$$$\mathrm{0}\leqslant\left({f}_{\mathrm{2}} \left({x}\right)=\mathrm{3}\left(\mathrm{1}−\mathrm{sin}\:{x}\right)\right)\leqslant\mathrm{6} \\ $$$${x}\in\left[−\frac{\mathrm{7}}{\mathrm{2}};\:\frac{\mathrm{5}}{\mathrm{2}}\right]:\:\mathrm{5}\leqslant{f}_{\mathrm{1}} \left({x}\right)\leqslant\mathrm{6}\:\Rightarrow \\ $$$$\mathrm{Solutions}\:\mathrm{possible}\:\mathrm{within}\:\mathrm{this}\:\mathrm{interval}\:\Rightarrow \\ $$$$\mathrm{2}\:\mathrm{solutions}: \\ $$$${x}_{\mathrm{1}} =−\pi+\mathrm{sin}^{−\mathrm{1}} \:\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${x}_{\mathrm{2}} =−\mathrm{sin}^{−\mathrm{1}} \:\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by SLVR last updated on 19/Apr/23

$${thanks}\:{sir} \\ $$
Answered by mr W last updated on 19/Apr/23
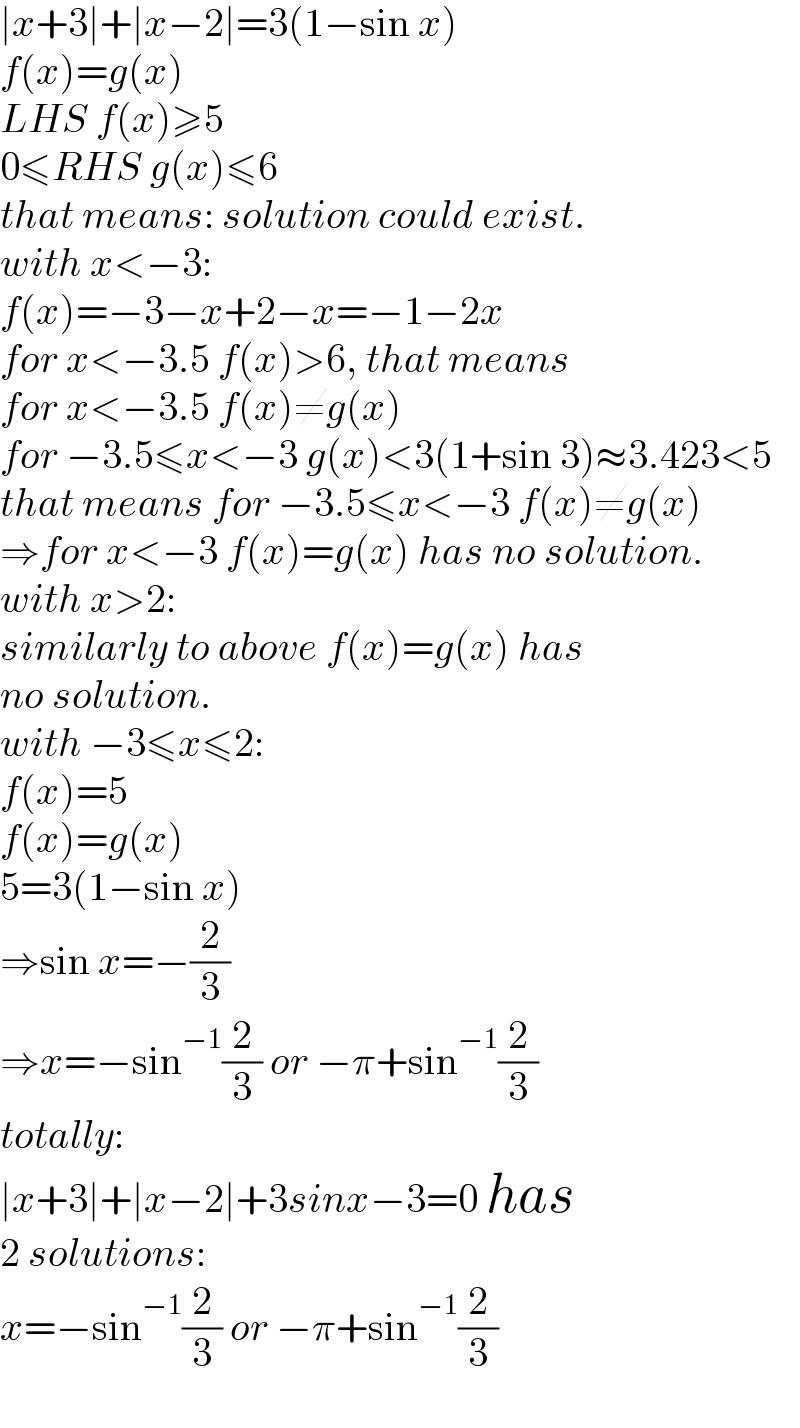
$$\mid{x}+\mathrm{3}\mid+\mid{x}−\mathrm{2}\mid=\mathrm{3}\left(\mathrm{1}−\mathrm{sin}\:{x}\right) \\ $$$${f}\left({x}\right)={g}\left({x}\right) \\ $$$${LHS}\:{f}\left({x}\right)\geqslant\mathrm{5} \\ $$$$\mathrm{0}\leqslant{RHS}\:{g}\left({x}\right)\leqslant\mathrm{6} \\ $$$${that}\:{means}:\:{solution}\:{could}\:{exist}. \\ $$$${with}\:{x}<−\mathrm{3}: \\ $$$${f}\left({x}\right)=−\mathrm{3}−{x}+\mathrm{2}−{x}=−\mathrm{1}−\mathrm{2}{x} \\ $$$${for}\:{x}<−\mathrm{3}.\mathrm{5}\:{f}\left({x}\right)>\mathrm{6},\:{that}\:{means} \\ $$$${for}\:{x}<−\mathrm{3}.\mathrm{5}\:{f}\left({x}\right)\neq{g}\left({x}\right) \\ $$$${for}\:−\mathrm{3}.\mathrm{5}\leqslant{x}<−\mathrm{3}\:{g}\left({x}\right)<\mathrm{3}\left(\mathrm{1}+\mathrm{sin}\:\mathrm{3}\right)\approx\mathrm{3}.\mathrm{423}<\mathrm{5} \\ $$$${that}\:{means}\:{for}\:−\mathrm{3}.\mathrm{5}\leqslant{x}<−\mathrm{3}\:{f}\left({x}\right)\neq{g}\left({x}\right) \\ $$$$\Rightarrow{for}\:{x}<−\mathrm{3}\:{f}\left({x}\right)={g}\left({x}\right)\:{has}\:{no}\:{solution}. \\ $$$${with}\:{x}>\mathrm{2}: \\ $$$${similarly}\:{to}\:{above}\:{f}\left({x}\right)={g}\left({x}\right)\:{has} \\ $$$${no}\:{solution}. \\ $$$${with}\:−\mathrm{3}\leqslant{x}\leqslant\mathrm{2}: \\ $$$${f}\left({x}\right)=\mathrm{5} \\ $$$${f}\left({x}\right)={g}\left({x}\right) \\ $$$$\mathrm{5}=\mathrm{3}\left(\mathrm{1}−\mathrm{sin}\:{x}\right) \\ $$$$\Rightarrow\mathrm{sin}\:{x}=−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\Rightarrow{x}=−\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{2}}{\mathrm{3}}\:{or}\:−\pi+\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{2}}{\mathrm{3}} \\ $$$${totally}: \\ $$$$\mid{x}+\mathrm{3}\mid+\mid{x}−\mathrm{2}\mid+\mathrm{3}{sinx}−\mathrm{3}=\mathrm{0}\:{has} \\ $$$$\mathrm{2}\:{solutions}: \\ $$$${x}=−\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{2}}{\mathrm{3}}\:{or}\:−\pi+\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by SLVR last updated on 19/Apr/23
$${Thanks}\:{a}\:{lot}..{Prof}.{W} \\ $$$${god}\:{bless}\:{you}\:{sir} \\ $$
Answered by mehdee42 last updated on 19/Apr/23
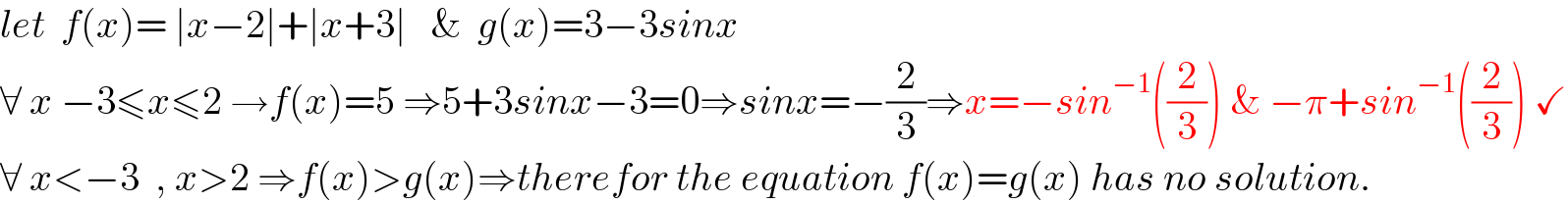
$${let}\:\:{f}\left({x}\right)=\:\mid{x}−\mathrm{2}\mid+\mid{x}+\mathrm{3}\mid\:\:\:\&\:\:{g}\left({x}\right)=\mathrm{3}−\mathrm{3}{sinx} \\ $$$$\forall\:{x}\:−\mathrm{3}\leqslant{x}\leqslant\mathrm{2}\:\rightarrow{f}\left({x}\right)=\mathrm{5}\:\Rightarrow\mathrm{5}+\mathrm{3}{sinx}−\mathrm{3}=\mathrm{0}\Rightarrow{sinx}=−\frac{\mathrm{2}}{\mathrm{3}}\Rightarrow{x}=−{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\mathrm{3}}\right)\:\&\:−\pi+{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\mathrm{3}}\right)\:\checkmark \\ $$$$\forall\:{x}<−\mathrm{3}\:\:,\:{x}>\mathrm{2}\:\Rightarrow{f}\left({x}\right)>{g}\left({x}\right)\Rightarrow{therefor}\:{the}\:{equation}\:{f}\left({x}\right)={g}\left({x}\right)\:{has}\:{no}\:{solution}. \\ $$
Commented by mehdee42 last updated on 19/Apr/23