Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 189531 by cortano12 last updated on 18/Mar/23

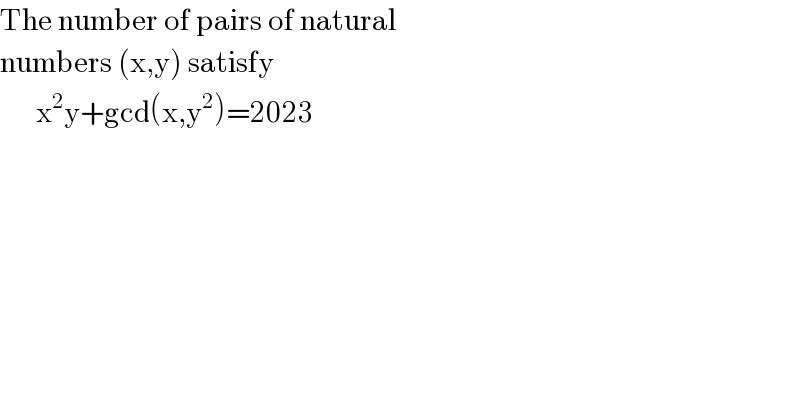
The number of pairs of natural numbers (x,y) satisfy x^2 y+gcd(x,y^2 )=2023

$$\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{pairs}\:\mathrm{of}\:\mathrm{natural} \\ $$$$\mathrm{numbers}\:\left(\mathrm{x},\mathrm{y}\right)\:\mathrm{satisfy} \\ $$$$\:\:\:\:\:\:\mathrm{x}^{\mathrm{2}} \mathrm{y}+\mathrm{gcd}\left(\mathrm{x},\mathrm{y}^{\mathrm{2}} \right)=\mathrm{2023} \\ $$

Answered by aleks041103 last updated on 19/Mar/23

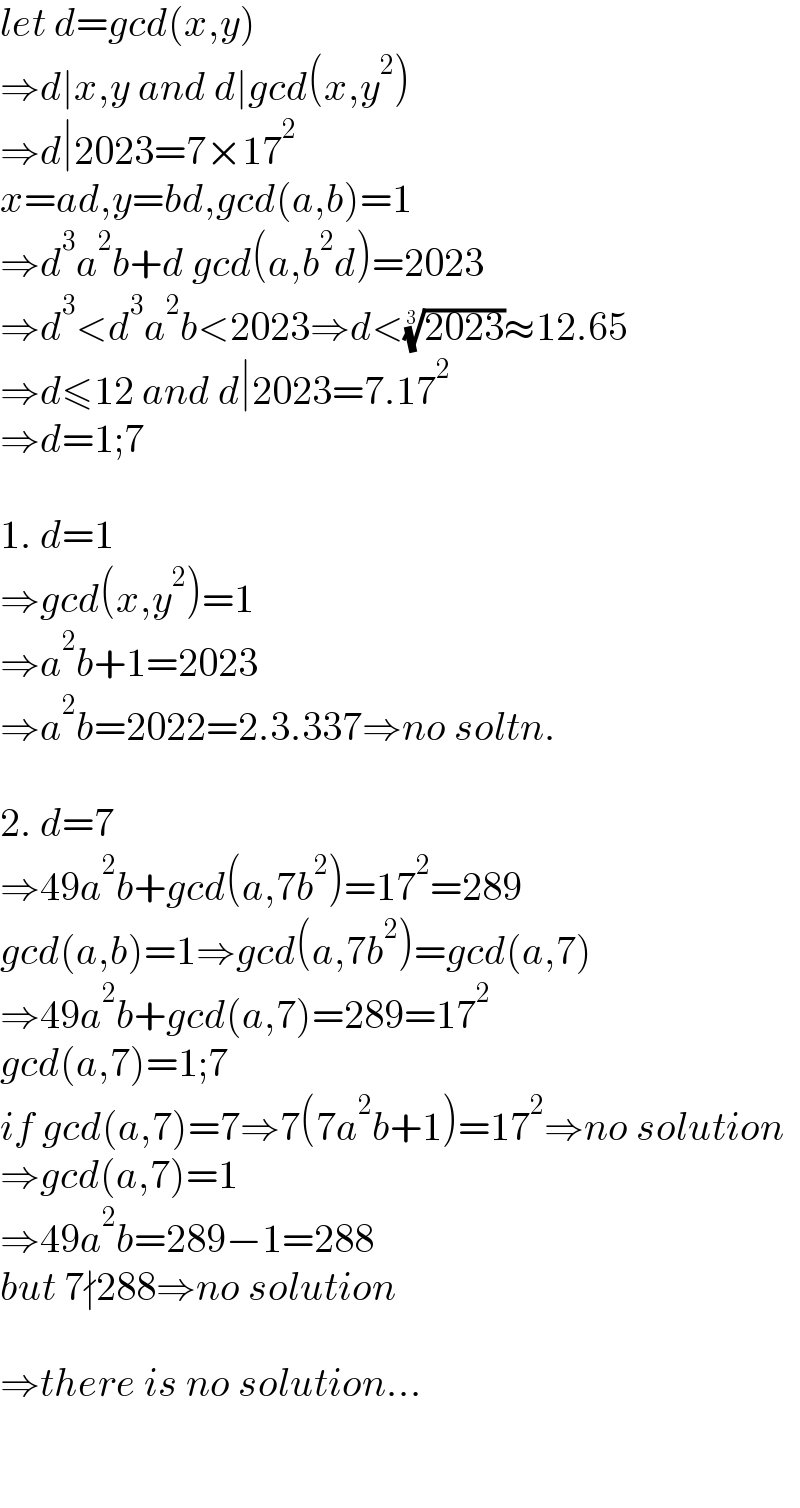
let d=gcd(x,y) ⇒d∣x,y and d∣gcd(x,y^2 ) ⇒d∣2023=7×17^2 x=ad,y=bd,gcd(a,b)=1 ⇒d^3 a^2 b+d gcd(a,b^2 d)=2023 ⇒d^3 <d^3 a^2 b<2023⇒d<((2023))^(1/3) ≈12.65 ⇒d≤12 and d∣2023=7.17^2 ⇒d=1;7 1. d=1 ⇒gcd(x,y^2 )=1 ⇒a^2 b+1=2023 ⇒a^2 b=2022=2.3.337⇒no soltn. 2. d=7 ⇒49a^2 b+gcd(a,7b^2 )=17^2 =289 gcd(a,b)=1⇒gcd(a,7b^2 )=gcd(a,7) ⇒49a^2 b+gcd(a,7)=289=17^2 gcd(a,7)=1;7 if gcd(a,7)=7⇒7(7a^2 b+1)=17^2 ⇒no solution ⇒gcd(a,7)=1 ⇒49a^2 b=289−1=288 but 7∤288⇒no solution ⇒there is no solution...

$${let}\:{d}={gcd}\left({x},{y}\right) \\ $$$$\Rightarrow{d}\mid{x},{y}\:{and}\:{d}\mid{gcd}\left({x},{y}^{\mathrm{2}} \right) \\ $$$$\Rightarrow{d}\mid\mathrm{2023}=\mathrm{7}×\mathrm{17}^{\mathrm{2}} \\ $$$${x}={ad},{y}={bd},{gcd}\left({a},{b}\right)=\mathrm{1} \\ $$$$\Rightarrow{d}^{\mathrm{3}} {a}^{\mathrm{2}} {b}+{d}\:{gcd}\left({a},{b}^{\mathrm{2}} {d}\right)=\mathrm{2023} \\ $$$$\Rightarrow{d}^{\mathrm{3}} <{d}^{\mathrm{3}} {a}^{\mathrm{2}} {b}<\mathrm{2023}\Rightarrow{d}<\sqrt[{\mathrm{3}}]{\mathrm{2023}}\approx\mathrm{12}.\mathrm{65} \\ $$$$\Rightarrow{d}\leqslant\mathrm{12}\:{and}\:{d}\mid\mathrm{2023}=\mathrm{7}.\mathrm{17}^{\mathrm{2}} \\ $$$$\Rightarrow{d}=\mathrm{1};\mathrm{7} \\ $$$$ \\ $$$$\mathrm{1}.\:{d}=\mathrm{1} \\ $$$$\Rightarrow{gcd}\left({x},{y}^{\mathrm{2}} \right)=\mathrm{1} \\ $$$$\Rightarrow{a}^{\mathrm{2}} {b}+\mathrm{1}=\mathrm{2023} \\ $$$$\Rightarrow{a}^{\mathrm{2}} {b}=\mathrm{2022}=\mathrm{2}.\mathrm{3}.\mathrm{337}\Rightarrow{no}\:{soltn}. \\ $$$$ \\ $$$$\mathrm{2}.\:{d}=\mathrm{7} \\ $$$$\Rightarrow\mathrm{49}{a}^{\mathrm{2}} {b}+{gcd}\left({a},\mathrm{7}{b}^{\mathrm{2}} \right)=\mathrm{17}^{\mathrm{2}} =\mathrm{289} \\ $$$${gcd}\left({a},{b}\right)=\mathrm{1}\Rightarrow{gcd}\left({a},\mathrm{7}{b}^{\mathrm{2}} \right)={gcd}\left({a},\mathrm{7}\right) \\ $$$$\Rightarrow\mathrm{49}{a}^{\mathrm{2}} {b}+{gcd}\left({a},\mathrm{7}\right)=\mathrm{289}=\mathrm{17}^{\mathrm{2}} \\ $$$${gcd}\left({a},\mathrm{7}\right)=\mathrm{1};\mathrm{7} \\ $$$${if}\:{gcd}\left({a},\mathrm{7}\right)=\mathrm{7}\Rightarrow\mathrm{7}\left(\mathrm{7}{a}^{\mathrm{2}} {b}+\mathrm{1}\right)=\mathrm{17}^{\mathrm{2}} \Rightarrow{no}\:{solution} \\ $$$$\Rightarrow{gcd}\left({a},\mathrm{7}\right)=\mathrm{1} \\ $$$$\Rightarrow\mathrm{49}{a}^{\mathrm{2}} {b}=\mathrm{289}−\mathrm{1}=\mathrm{288} \\ $$$${but}\:\mathrm{7}\nmid\mathrm{288}\Rightarrow{no}\:{solution} \\ $$$$ \\ $$$$\Rightarrow{there}\:{is}\:{no}\:{solution}... \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com