Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 10195 by priyank last updated on 30/Jan/17

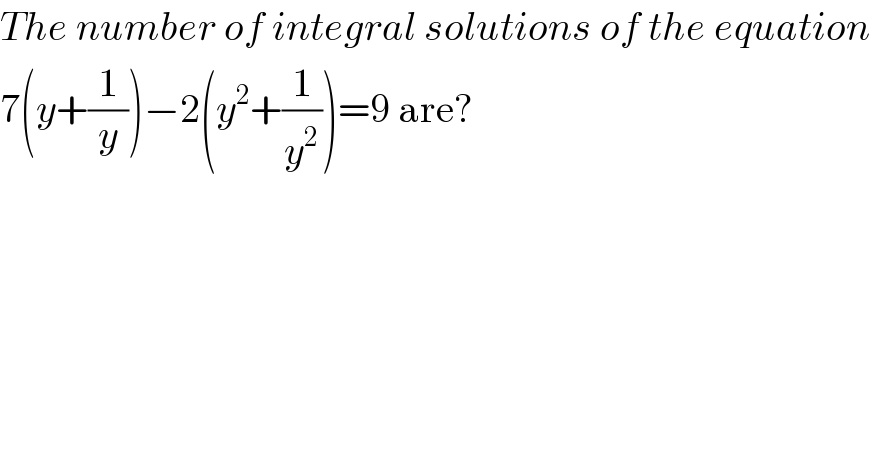
The number of integral solutions of the equation 7(y+(1/y))−2(y^2 +(1/y^2 ))=9 are?

$${The}\:{number}\:{of}\:{integral}\:{solutions}\:{of}\:{the}\:{equation}\: \\ $$$$\mathrm{7}\left({y}+\frac{\mathrm{1}}{{y}}\right)−\mathrm{2}\left({y}^{\mathrm{2}} +\frac{\mathrm{1}}{{y}^{\mathrm{2}} }\right)=\mathrm{9}\:\mathrm{are}? \\ $$

Commented by prakash jain last updated on 30/Jan/17

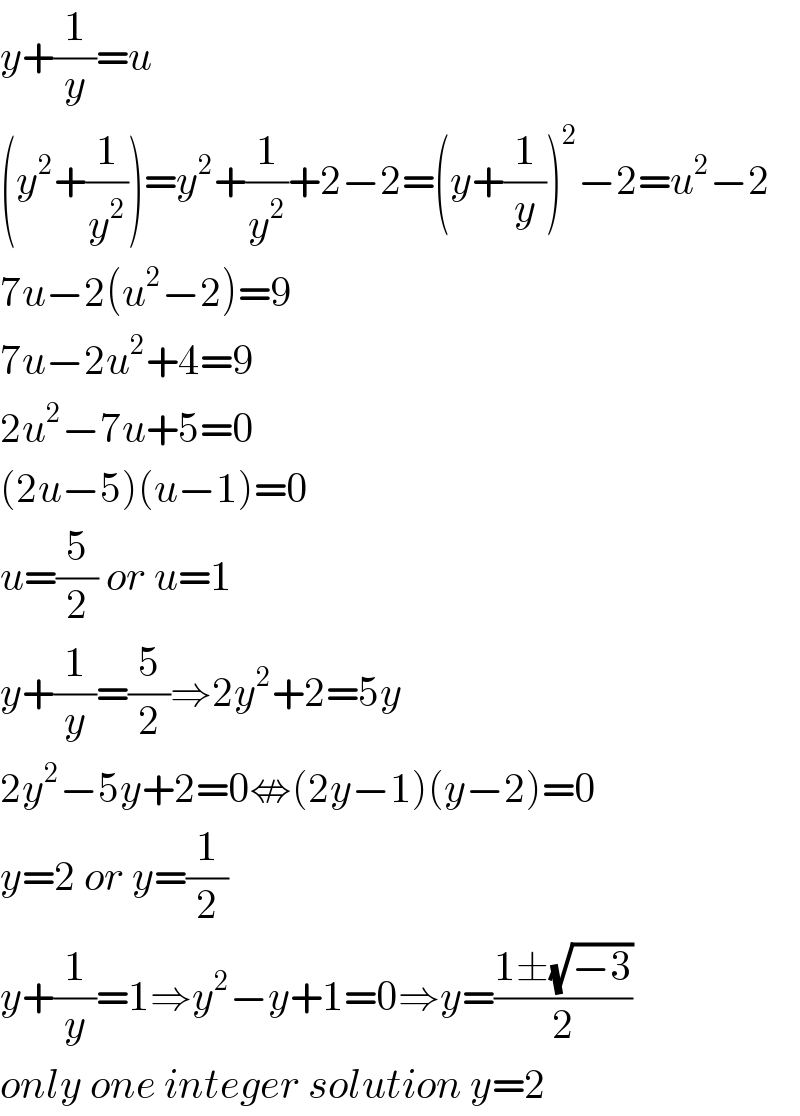
y+(1/y)=u (y^2 +(1/y^2 ))=y^2 +(1/y^2 )+2−2=(y+(1/y))^2 −2=u^2 −2 7u−2(u^2 −2)=9 7u−2u^2 +4=9 2u^2 −7u+5=0 (2u−5)(u−1)=0 u=(5/2) or u=1 y+(1/y)=(5/2)⇒2y^2 +2=5y 2y^2 −5y+2=0⇎(2y−1)(y−2)=0 y=2 or y=(1/2) y+(1/y)=1⇒y^2 −y+1=0⇒y=((1±(√(−3)))/2) only one integer solution y=2

$${y}+\frac{\mathrm{1}}{{y}}={u} \\ $$$$\left({y}^{\mathrm{2}} +\frac{\mathrm{1}}{{y}^{\mathrm{2}} }\right)={y}^{\mathrm{2}} +\frac{\mathrm{1}}{{y}^{\mathrm{2}} }+\mathrm{2}−\mathrm{2}=\left({y}+\frac{\mathrm{1}}{{y}}\right)^{\mathrm{2}} −\mathrm{2}={u}^{\mathrm{2}} −\mathrm{2} \\ $$$$\mathrm{7}{u}−\mathrm{2}\left({u}^{\mathrm{2}} −\mathrm{2}\right)=\mathrm{9} \\ $$$$\mathrm{7}{u}−\mathrm{2}{u}^{\mathrm{2}} +\mathrm{4}=\mathrm{9} \\ $$$$\mathrm{2}{u}^{\mathrm{2}} −\mathrm{7}{u}+\mathrm{5}=\mathrm{0} \\ $$$$\left(\mathrm{2}{u}−\mathrm{5}\right)\left({u}−\mathrm{1}\right)=\mathrm{0} \\ $$$${u}=\frac{\mathrm{5}}{\mathrm{2}}\:{or}\:{u}=\mathrm{1} \\ $$$${y}+\frac{\mathrm{1}}{{y}}=\frac{\mathrm{5}}{\mathrm{2}}\Rightarrow\mathrm{2}{y}^{\mathrm{2}} +\mathrm{2}=\mathrm{5}{y} \\ $$$$\mathrm{2}{y}^{\mathrm{2}} −\mathrm{5}{y}+\mathrm{2}=\mathrm{0}\nLeftrightarrow\left(\mathrm{2}{y}−\mathrm{1}\right)\left({y}−\mathrm{2}\right)=\mathrm{0} \\ $$$${y}=\mathrm{2}\:{or}\:{y}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${y}+\frac{\mathrm{1}}{{y}}=\mathrm{1}\Rightarrow{y}^{\mathrm{2}} −{y}+\mathrm{1}=\mathrm{0}\Rightarrow{y}=\frac{\mathrm{1}\pm\sqrt{−\mathrm{3}}}{\mathrm{2}} \\ $$$${only}\:{one}\:{integer}\:{solution}\:{y}=\mathrm{2} \\ $$

Answered by FilupSmith last updated on 30/Jan/17

Do you mean integer solution? 7y+(7/y)−2y^2 −(2/y^2 )=9 7y^3 +7y−2y^4 −2=9y^2 −2y^4 +7y^3 −9y^2 +7y−2=0 2y^4 −7y^3 +9y^2 −7y+2=0 (2y−1)(y−2)(y^2 −y+1)=0 (from wolfram alpha) (1) 2y=1 ⇒ y=(1/2) (2) y=2 (3) y=((1±i(√3))/2) ∴ y has 1 integer root

$$\mathrm{Do}\:\mathrm{you}\:\mathrm{mean}\:\mathrm{integer}\:\mathrm{solution}? \\ $$$$\: \\ $$$$\mathrm{7}{y}+\frac{\mathrm{7}}{{y}}−\mathrm{2}{y}^{\mathrm{2}} −\frac{\mathrm{2}}{{y}^{\mathrm{2}} }=\mathrm{9} \\ $$$$\mathrm{7}{y}^{\mathrm{3}} +\mathrm{7}{y}−\mathrm{2}{y}^{\mathrm{4}} −\mathrm{2}=\mathrm{9}{y}^{\mathrm{2}} \\ $$$$−\mathrm{2}{y}^{\mathrm{4}} +\mathrm{7}{y}^{\mathrm{3}} −\mathrm{9}{y}^{\mathrm{2}} +\mathrm{7}{y}−\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{2}{y}^{\mathrm{4}} −\mathrm{7}{y}^{\mathrm{3}} +\mathrm{9}{y}^{\mathrm{2}} −\mathrm{7}{y}+\mathrm{2}=\mathrm{0} \\ $$$$\left(\mathrm{2}{y}−\mathrm{1}\right)\left({y}−\mathrm{2}\right)\left({y}^{\mathrm{2}} −{y}+\mathrm{1}\right)=\mathrm{0}\:\:\:\:\:\:\left(\mathrm{from}\:\mathrm{wolfram}\:\mathrm{alpha}\right) \\ $$$$\left(\mathrm{1}\right)\:\:\:\mathrm{2}{y}=\mathrm{1}\:\Rightarrow\:{y}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\:\:\:{y}=\mathrm{2} \\ $$$$\left(\mathrm{3}\right)\:\:\:{y}=\frac{\mathrm{1}\pm{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\: \\ $$$$\therefore\:{y}\:\mathrm{has}\:\mathrm{1}\:\mathrm{integer}\:\mathrm{root} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com