
Question Number 212342 by hardmath last updated on 10/Oct/24
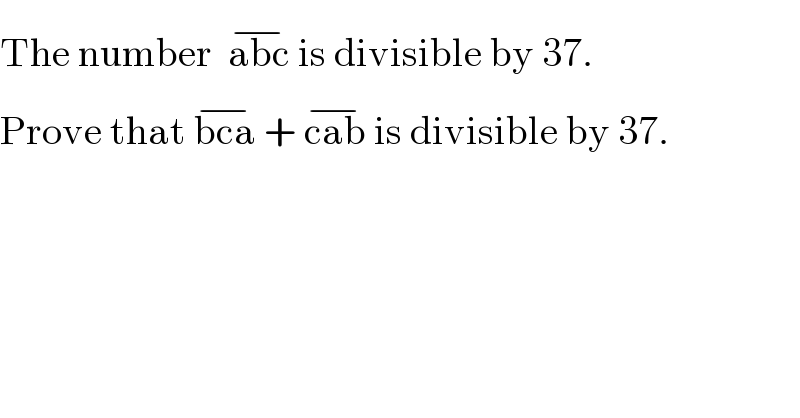
$$\mathrm{The}\:\mathrm{number}\:\:\overline {\mathrm{abc}}\:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{37}. \\ $$$$\mathrm{Prove}\:\mathrm{that}\:\overline {\mathrm{bca}}\:+\:\overline {\mathrm{cab}}\:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{37}.\: \\ $$
Answered by A5T last updated on 10/Oct/24
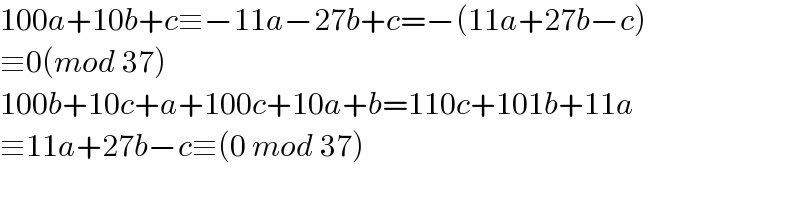
$$\mathrm{100}{a}+\mathrm{10}{b}+{c}\equiv−\mathrm{11}{a}−\mathrm{27}{b}+{c}=−\left(\mathrm{11}{a}+\mathrm{27}{b}−{c}\right) \\ $$$$\equiv\mathrm{0}\left({mod}\:\mathrm{37}\right) \\ $$$$\mathrm{100}{b}+\mathrm{10}{c}+{a}+\mathrm{100}{c}+\mathrm{10}{a}+{b}=\mathrm{110}{c}+\mathrm{101}{b}+\mathrm{11}{a} \\ $$$$\equiv\mathrm{11}{a}+\mathrm{27}{b}−{c}\equiv\left(\mathrm{0}\:{mod}\:\mathrm{37}\right) \\ $$
