
Question Number 482 by prakash jain last updated on 12/Jan/15

$$\mathrm{The}\:\mathrm{number}\:\mathrm{1000}!\:\mathrm{has}\:\mathrm{certain}\:\mathrm{number} \\ $$$$\mathrm{of}\:\mathrm{0}{s}\:\mathrm{at}\:\mathrm{the}\:\mathrm{end},\:\mathrm{what}\:\mathrm{the}\:\mathrm{the}\:\mathrm{first}\:\mathrm{non}−\mathrm{zero} \\ $$$$\mathrm{digit}. \\ $$$$\mathrm{1000}!=...\mathrm{d}_{\mathrm{1}} \mathrm{d}_{\mathrm{2}} \mathrm{d}_{\mathrm{3}} \mathrm{D00000}... \\ $$$$\mathrm{where}\:\mathrm{d}_{\mathrm{1}} ,\mathrm{d}_{\mathrm{2}} ,\mathrm{d}_{\mathrm{3}} ,\mathrm{D}\:\mathrm{are}\:\mathrm{digits}. \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{digit}\:\mathrm{D}. \\ $$
Commented by 123456 last updated on 12/Jan/15
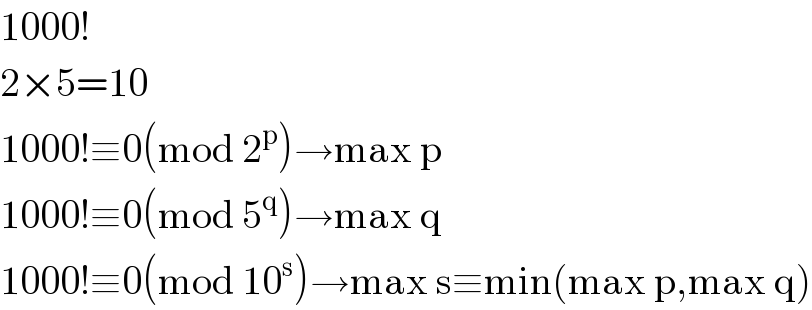
$$\mathrm{1000}! \\ $$$$\mathrm{2}×\mathrm{5}=\mathrm{10} \\ $$$$\mathrm{1000}!\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{2}^{\mathrm{p}} \right)\rightarrow\mathrm{max}\:\mathrm{p} \\ $$$$\mathrm{1000}!\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{5}^{\mathrm{q}} \right)\rightarrow\mathrm{max}\:\mathrm{q} \\ $$$$\mathrm{1000}!\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{10}^{\mathrm{s}} \right)\rightarrow\mathrm{max}\:\mathrm{s}\equiv\mathrm{min}\left(\mathrm{max}\:\mathrm{p},\mathrm{max}\:\mathrm{q}\right) \\ $$
