Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 16740 by Tinkutara last updated on 26/Jun/17

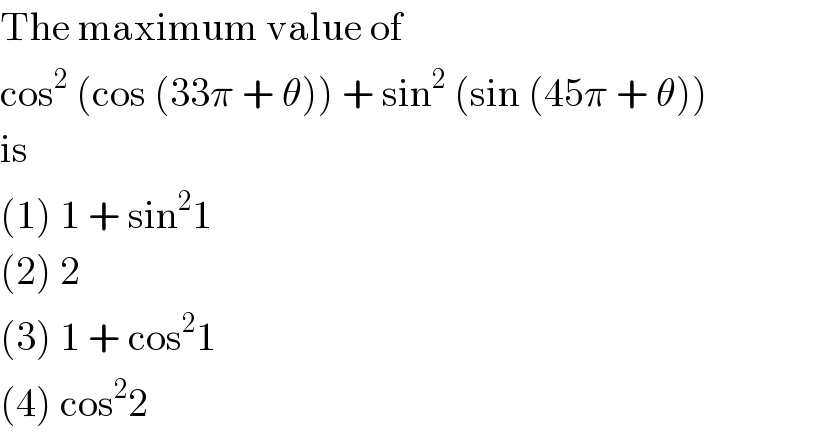
The maximum value of cos^2 (cos (33π + θ)) + sin^2 (sin (45π + θ)) is (1) 1 + sin^2 1 (2) 2 (3) 1 + cos^2 1 (4) cos^2 2

$$\mathrm{The}\:\mathrm{maximum}\:\mathrm{value}\:\mathrm{of} \\ $$$$\mathrm{cos}^{\mathrm{2}} \:\left(\mathrm{cos}\:\left(\mathrm{33}\pi\:+\:\theta\right)\right)\:+\:\mathrm{sin}^{\mathrm{2}} \:\left(\mathrm{sin}\:\left(\mathrm{45}\pi\:+\:\theta\right)\right) \\ $$$$\mathrm{is} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{1}\:+\:\mathrm{sin}^{\mathrm{2}} \mathrm{1} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{2} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{1}\:+\:\mathrm{cos}^{\mathrm{2}} \mathrm{1} \\ $$$$\left(\mathrm{4}\right)\:\mathrm{cos}^{\mathrm{2}} \mathrm{2} \\ $$

Commented by ajfour last updated on 26/Jun/17

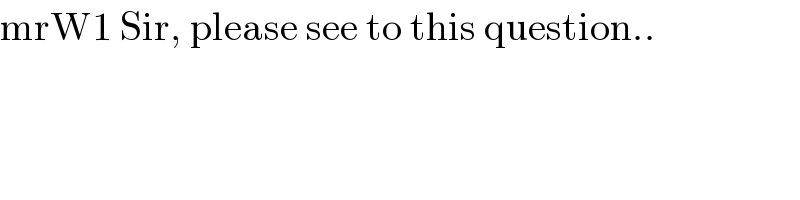
mrW1 Sir, please see to this question..

$$\mathrm{mrW1}\:\mathrm{Sir},\:\mathrm{please}\:\mathrm{see}\:\mathrm{to}\:\mathrm{this}\:\mathrm{question}.. \\ $$

Commented by Tinkutara last updated on 26/Jun/17

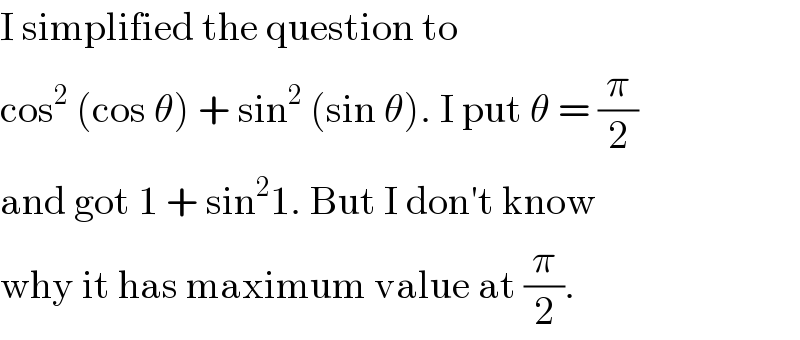
I simplified the question to cos^2 (cos θ) + sin^2 (sin θ). I put θ = (π/2) and got 1 + sin^2 1. But I don′t know why it has maximum value at (π/2).

$$\mathrm{I}\:\mathrm{simplified}\:\mathrm{the}\:\mathrm{question}\:\mathrm{to} \\ $$$$\mathrm{cos}^{\mathrm{2}} \:\left(\mathrm{cos}\:\theta\right)\:+\:\mathrm{sin}^{\mathrm{2}} \:\left(\mathrm{sin}\:\theta\right).\:\mathrm{I}\:\mathrm{put}\:\theta\:=\:\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{and}\:\mathrm{got}\:\mathrm{1}\:+\:\mathrm{sin}^{\mathrm{2}} \mathrm{1}.\:\mathrm{But}\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know} \\ $$$$\mathrm{why}\:\mathrm{it}\:\mathrm{has}\:\mathrm{maximum}\:\mathrm{value}\:\mathrm{at}\:\frac{\pi}{\mathrm{2}}. \\ $$

Commented by prakash jain last updated on 26/Jun/17

u=cos^2 (cos θ)+sin^2 (sin θ) =1+(1/2)(cos (2cos θ)−cos (2sin θ)) u′=sin θsin (2cos θ)+cos θsin (2sin θ) =sin θ{(2cos θ)−(((2cosθ)^3 )/(3!))+...}+ +cos θ{(2sin θ)−(((2sin θ)^3 )/(3!))+−..} =sin 2θ[{1−(((2cos θ)^2 )/(3!))+..}+{1−(((2sin θ)^2 )/(3!))+..}] u′=0 when sin 2θ=0⇒ θ=0, (π/2) double derivate will give us whether it is maxima or minima. 0 minima (π/2) maxima

$${u}=\mathrm{cos}^{\mathrm{2}} \left(\mathrm{cos}\:\theta\right)+\mathrm{sin}^{\mathrm{2}} \left(\mathrm{sin}\:\theta\right) \\ $$$$=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}\:\left(\mathrm{2cos}\:\theta\right)−\mathrm{cos}\:\left(\mathrm{2sin}\:\theta\right)\right) \\ $$$${u}'=\mathrm{sin}\:\theta\mathrm{sin}\:\left(\mathrm{2cos}\:\theta\right)+\mathrm{cos}\:\theta\mathrm{sin}\:\left(\mathrm{2sin}\:\theta\right) \\ $$$$=\mathrm{sin}\:\theta\left\{\left(\mathrm{2cos}\:\theta\right)−\frac{\left(\mathrm{2cos}\theta\right)^{\mathrm{3}} }{\mathrm{3}!}+...\right\}+ \\ $$$$+\mathrm{cos}\:\theta\left\{\left(\mathrm{2sin}\:\theta\right)−\frac{\left(\mathrm{2sin}\:\theta\right)^{\mathrm{3}} }{\mathrm{3}!}+−..\right\} \\ $$$$=\mathrm{sin}\:\mathrm{2}\theta\left[\left\{\mathrm{1}−\frac{\left(\mathrm{2cos}\:\theta\right)^{\mathrm{2}} }{\mathrm{3}!}+..\right\}+\left\{\mathrm{1}−\frac{\left(\mathrm{2sin}\:\theta\right)^{\mathrm{2}} }{\mathrm{3}!}+..\right\}\right] \\ $$$${u}'=\mathrm{0}\:\mathrm{when}\:\mathrm{sin}\:\mathrm{2}\theta=\mathrm{0}\Rightarrow\:\theta=\mathrm{0},\:\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{double}\:\mathrm{derivate}\:\mathrm{will}\:\mathrm{give}\:\mathrm{us} \\ $$$$\mathrm{whether}\:\mathrm{it}\:\mathrm{is}\:\mathrm{maxima}\:\mathrm{or}\:\mathrm{minima}. \\ $$$$\mathrm{0}\:\mathrm{minima} \\ $$$$\frac{\pi}{\mathrm{2}}\:\mathrm{maxima} \\ $$

Answered by mrW1 last updated on 26/Jun/17

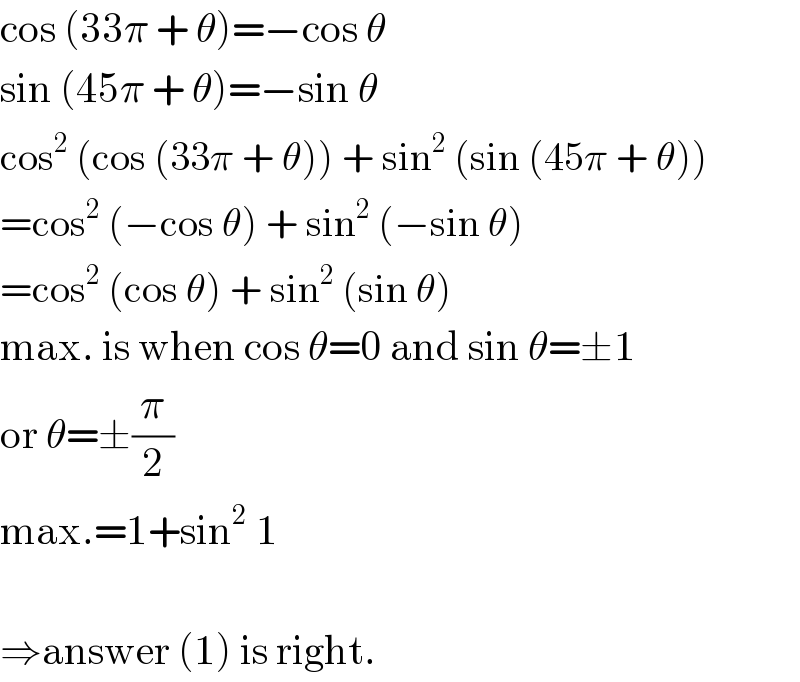
cos (33π + θ)=−cos θ sin (45π + θ)=−sin θ cos^2 (cos (33π + θ)) + sin^2 (sin (45π + θ)) =cos^2 (−cos θ) + sin^2 (−sin θ) =cos^2 (cos θ) + sin^2 (sin θ) max. is when cos θ=0 and sin θ=±1 or θ=±(π/2) max.=1+sin^2 1 ⇒answer (1) is right.

$$\mathrm{cos}\:\left(\mathrm{33}\pi\:+\:\theta\right)=−\mathrm{cos}\:\theta \\ $$$$\mathrm{sin}\:\left(\mathrm{45}\pi\:+\:\theta\right)=−\mathrm{sin}\:\theta \\ $$$$\mathrm{cos}^{\mathrm{2}} \:\left(\mathrm{cos}\:\left(\mathrm{33}\pi\:+\:\theta\right)\right)\:+\:\mathrm{sin}^{\mathrm{2}} \:\left(\mathrm{sin}\:\left(\mathrm{45}\pi\:+\:\theta\right)\right) \\ $$$$=\mathrm{cos}^{\mathrm{2}} \:\left(−\mathrm{cos}\:\theta\right)\:+\:\mathrm{sin}^{\mathrm{2}} \:\left(−\mathrm{sin}\:\theta\right) \\ $$$$=\mathrm{cos}^{\mathrm{2}} \:\left(\mathrm{cos}\:\theta\right)\:+\:\mathrm{sin}^{\mathrm{2}} \:\left(\mathrm{sin}\:\theta\right) \\ $$$$\mathrm{max}.\:\mathrm{is}\:\mathrm{when}\:\mathrm{cos}\:\theta=\mathrm{0}\:\mathrm{and}\:\mathrm{sin}\:\theta=\pm\mathrm{1} \\ $$$$\mathrm{or}\:\theta=\pm\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{max}.=\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:\mathrm{1} \\ $$$$ \\ $$$$\Rightarrow\mathrm{answer}\:\left(\mathrm{1}\right)\:\mathrm{is}\:\mathrm{right}. \\ $$

Commented by Tinkutara last updated on 26/Jun/17

Thanks Sir!

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Commented by ajfour last updated on 26/Jun/17

yes Sir, obviously!

$$\mathrm{yes}\:\mathrm{Sir},\:\mathrm{obviously}! \\ $$

Commented by Tinkutara last updated on 26/Jun/17

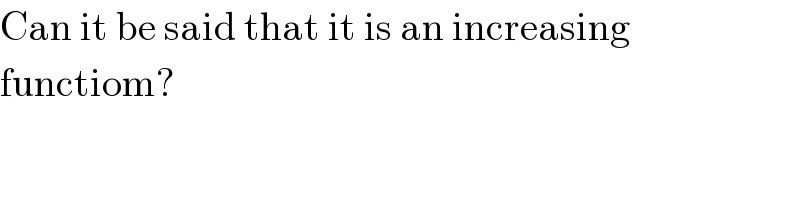
Can it be said that it is an increasing functiom?

$$\mathrm{Can}\:\mathrm{it}\:\mathrm{be}\:\mathrm{said}\:\mathrm{that}\:\mathrm{it}\:\mathrm{is}\:\mathrm{an}\:\mathrm{increasing} \\ $$$$\mathrm{functiom}? \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com