Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 76245 by vishalbhardwaj last updated on 25/Dec/19

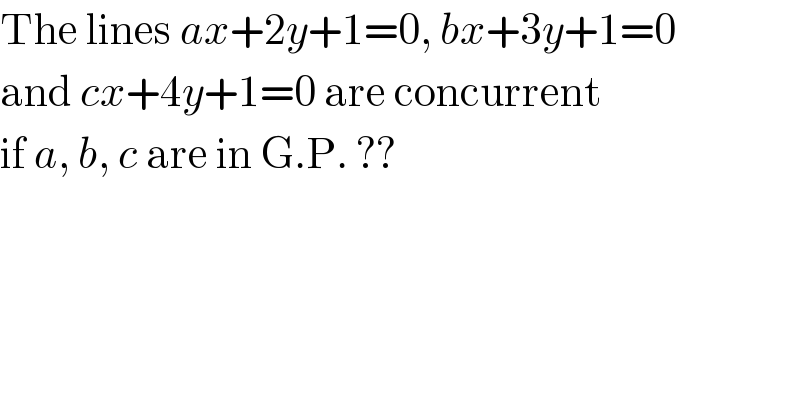
The lines ax+2y+1=0, bx+3y+1=0 and cx+4y+1=0 are concurrent if a, b, c are in G.P. ??

$$\mathrm{The}\:\mathrm{lines}\:{ax}+\mathrm{2}{y}+\mathrm{1}=\mathrm{0},\:{bx}+\mathrm{3}{y}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{and}\:{cx}+\mathrm{4}{y}+\mathrm{1}=\mathrm{0}\:\mathrm{are}\:\mathrm{concurrent} \\ $$$$\mathrm{if}\:{a},\:{b},\:{c}\:\mathrm{are}\:\mathrm{in}\:\mathrm{G}.\mathrm{P}.\:?? \\ $$

Answered by MJS last updated on 25/Dec/19

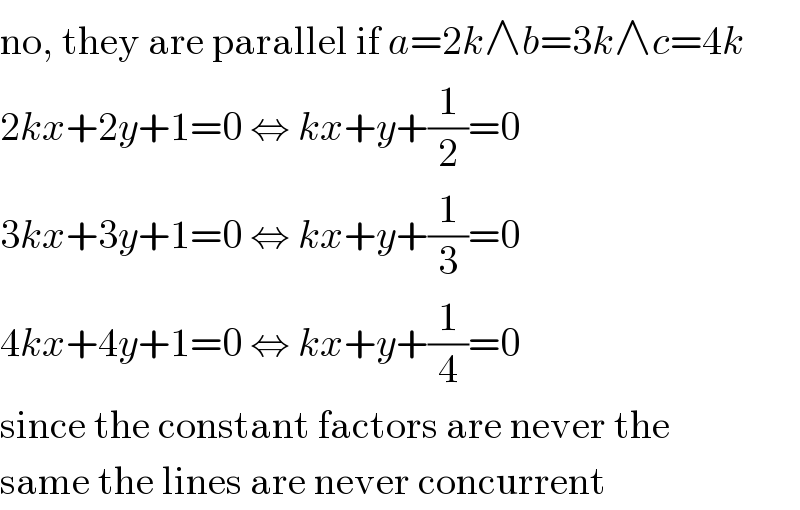
no, they are parallel if a=2k∧b=3k∧c=4k 2kx+2y+1=0 ⇔ kx+y+(1/2)=0 3kx+3y+1=0 ⇔ kx+y+(1/3)=0 4kx+4y+1=0 ⇔ kx+y+(1/4)=0 since the constant factors are never the same the lines are never concurrent

$$\mathrm{no},\:\mathrm{they}\:\mathrm{are}\:\mathrm{parallel}\:\mathrm{if}\:{a}=\mathrm{2}{k}\wedge{b}=\mathrm{3}{k}\wedge{c}=\mathrm{4}{k} \\ $$$$\mathrm{2}{kx}+\mathrm{2}{y}+\mathrm{1}=\mathrm{0}\:\Leftrightarrow\:{kx}+{y}+\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{0} \\ $$$$\mathrm{3}{kx}+\mathrm{3}{y}+\mathrm{1}=\mathrm{0}\:\Leftrightarrow\:{kx}+{y}+\frac{\mathrm{1}}{\mathrm{3}}=\mathrm{0} \\ $$$$\mathrm{4}{kx}+\mathrm{4}{y}+\mathrm{1}=\mathrm{0}\:\Leftrightarrow\:{kx}+{y}+\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{0} \\ $$$$\mathrm{since}\:\mathrm{the}\:\mathrm{constant}\:\mathrm{factors}\:\mathrm{are}\:\mathrm{never}\:\mathrm{the} \\ $$$$\mathrm{same}\:\mathrm{the}\:\mathrm{lines}\:\mathrm{are}\:\mathrm{never}\:\mathrm{concurrent} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com