
Question Number 25895 by Mr eaay last updated on 16/Dec/17

$${The}\:{hands}\:{of}\:{a}\:{clock}\:{have}\:{length}\:\mathrm{3}{cm}\: \\ $$$${and}\:\mathrm{5}{cm}.{Calculate}\:{the}\:{distance}\:{between} \\ $$$${the}\:{tips}\:{of}\:{the}\:{hand}\:{at}\:\mathrm{4}\:``\mathrm{0}''\:{clock}. \\ $$
Answered by mrW1 last updated on 16/Dec/17
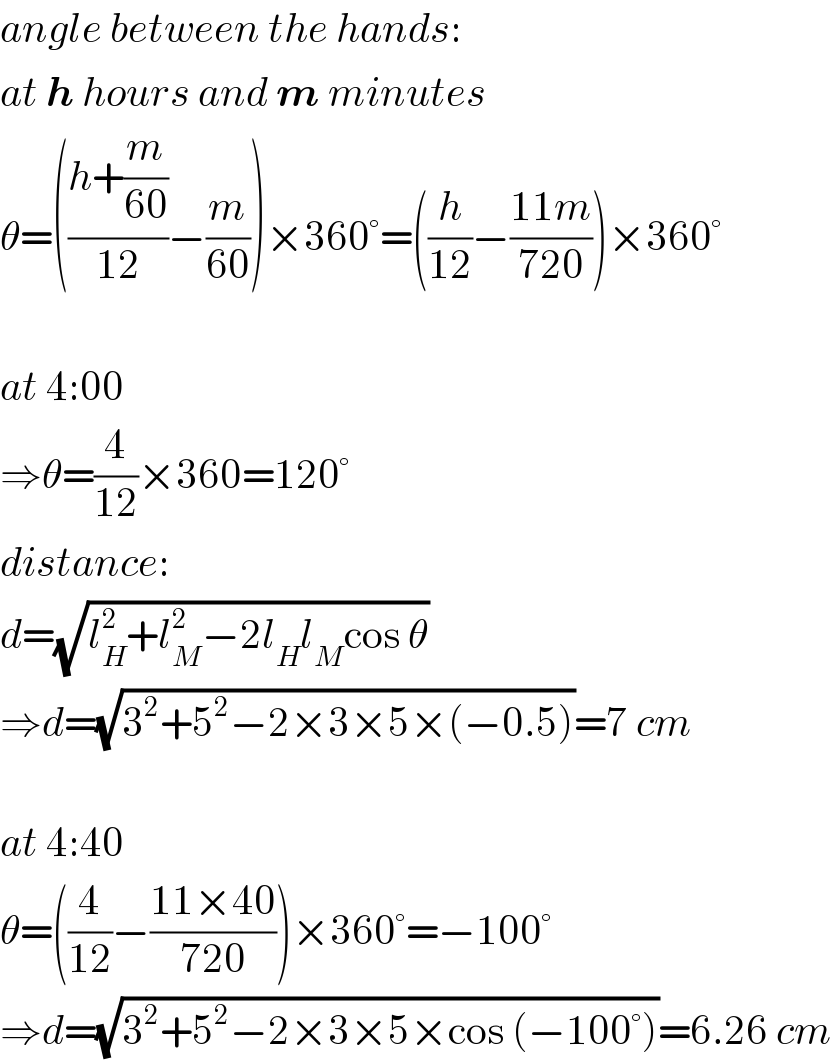
$${angle}\:{between}\:{the}\:{hands}: \\ $$$${at}\:\boldsymbol{{h}}\:{hours}\:{and}\:\boldsymbol{{m}}\:{minutes} \\ $$$$\theta=\left(\frac{{h}+\frac{{m}}{\mathrm{60}}}{\mathrm{12}}−\frac{{m}}{\mathrm{60}}\right)×\mathrm{360}°=\left(\frac{{h}}{\mathrm{12}}−\frac{\mathrm{11}{m}}{\mathrm{720}}\right)×\mathrm{360}° \\ $$$$ \\ $$$${at}\:\mathrm{4}:\mathrm{00} \\ $$$$\Rightarrow\theta=\frac{\mathrm{4}}{\mathrm{12}}×\mathrm{360}=\mathrm{120}° \\ $$$${distance}: \\ $$$${d}=\sqrt{{l}_{{H}} ^{\mathrm{2}} +{l}_{{M}} ^{\mathrm{2}} −\mathrm{2}{l}_{{H}} {l}_{{M}} \mathrm{cos}\:\theta} \\ $$$$\Rightarrow{d}=\sqrt{\mathrm{3}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} −\mathrm{2}×\mathrm{3}×\mathrm{5}×\left(−\mathrm{0}.\mathrm{5}\right)}=\mathrm{7}\:{cm} \\ $$$$ \\ $$$${at}\:\mathrm{4}:\mathrm{40} \\ $$$$\theta=\left(\frac{\mathrm{4}}{\mathrm{12}}−\frac{\mathrm{11}×\mathrm{40}}{\mathrm{720}}\right)×\mathrm{360}°=−\mathrm{100}° \\ $$$$\Rightarrow{d}=\sqrt{\mathrm{3}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} −\mathrm{2}×\mathrm{3}×\mathrm{5}×\mathrm{cos}\:\left(−\mathrm{100}°\right)}=\mathrm{6}.\mathrm{26}\:{cm} \\ $$
Commented by Mr eaay last updated on 16/Dec/17
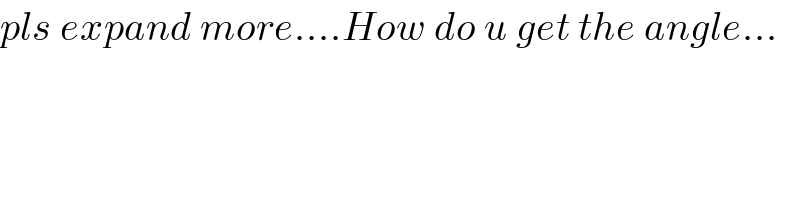
$${pls}\:{expand}\:{more}....{How}\:{do}\:{u}\:{get}\:{the}\:{angle}... \\ $$
Commented by mrW1 last updated on 16/Dec/17

$${at}\:\mathrm{4}:\mathrm{00}\:{the}\:{hour}\:{hand}\:{is}\:{at}\:{position}\:``\mathrm{4}'' \\ $$$${and}\:{the}\:{minute}\:{hand}\:{is}\:{at}\:{position}\:``\mathrm{0}''. \\ $$$$\mathrm{12}\:{hours}\:{mean}\:\mathrm{360}°,\:{so}\:\mathrm{4}\:{hours}\:{mean} \\ $$$$\mathrm{120}°. \\ $$
