
Question Number 14030 by Tinkutara last updated on 27/May/17
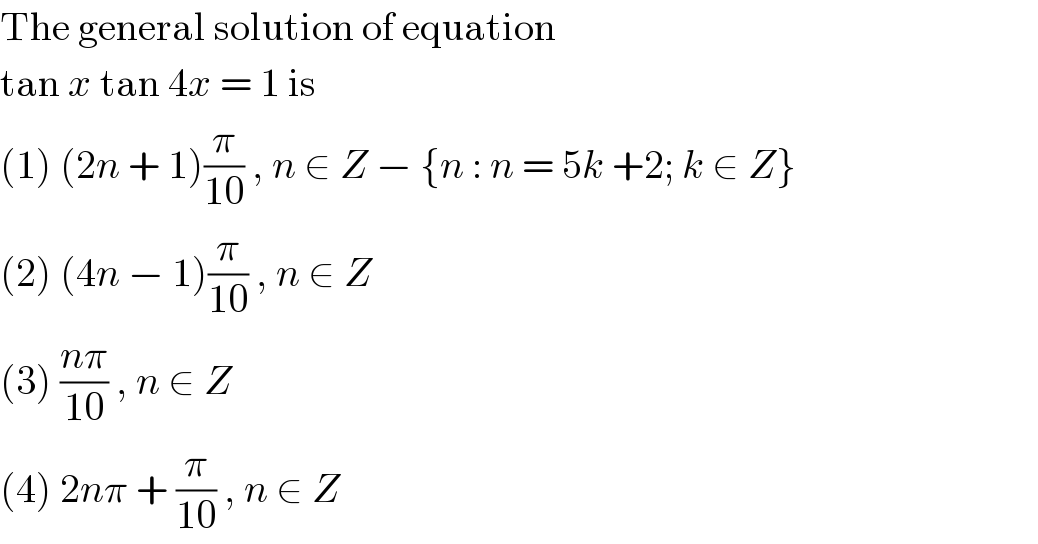
$$\mathrm{The}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{of}\:\mathrm{equation} \\ $$$$\mathrm{tan}\:{x}\:\mathrm{tan}\:\mathrm{4}{x}\:=\:\mathrm{1}\:\mathrm{is} \\ $$$$\left(\mathrm{1}\right)\:\left(\mathrm{2}{n}\:+\:\mathrm{1}\right)\frac{\pi}{\mathrm{10}}\:,\:{n}\:\in\:{Z}\:−\:\left\{{n}\::\:{n}\:=\:\mathrm{5}{k}\:+\mathrm{2};\:{k}\:\in\:{Z}\right\} \\ $$$$\left(\mathrm{2}\right)\:\left(\mathrm{4}{n}\:−\:\mathrm{1}\right)\frac{\pi}{\mathrm{10}}\:,\:{n}\:\in\:{Z} \\ $$$$\left(\mathrm{3}\right)\:\frac{{n}\pi}{\mathrm{10}}\:,\:{n}\:\in\:{Z} \\ $$$$\left(\mathrm{4}\right)\:\mathrm{2}{n}\pi\:+\:\frac{\pi}{\mathrm{10}}\:,\:{n}\:\in\:{Z} \\ $$
Answered by ajfour last updated on 27/May/17
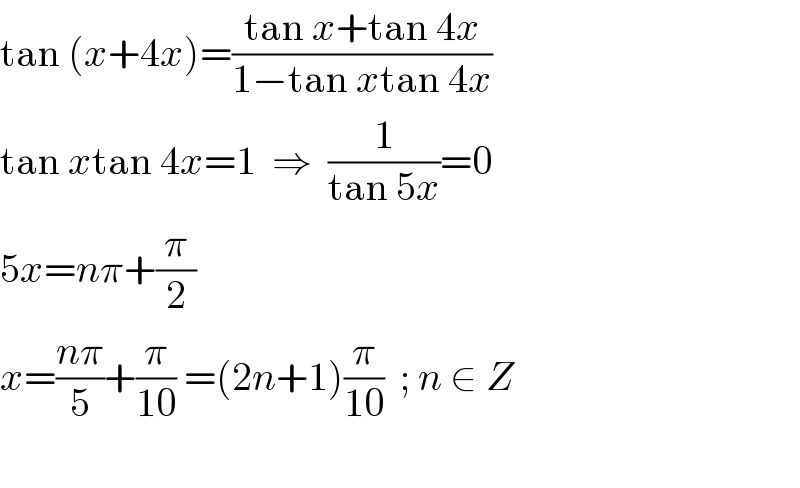
$$\mathrm{tan}\:\left({x}+\mathrm{4}{x}\right)=\frac{\mathrm{tan}\:{x}+\mathrm{tan}\:\mathrm{4}{x}}{\mathrm{1}−\mathrm{tan}\:{x}\mathrm{tan}\:\mathrm{4}{x}} \\ $$$$\mathrm{tan}\:{x}\mathrm{tan}\:\mathrm{4}{x}=\mathrm{1}\:\:\Rightarrow\:\:\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{5}{x}}=\mathrm{0} \\ $$$$\mathrm{5}{x}={n}\pi+\frac{\pi}{\mathrm{2}} \\ $$$${x}=\frac{{n}\pi}{\mathrm{5}}+\frac{\pi}{\mathrm{10}}\:=\left(\mathrm{2}{n}+\mathrm{1}\right)\frac{\pi}{\mathrm{10}}\:\:;\:{n}\:\in\:{Z} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
Commented by Tinkutara last updated on 27/May/17
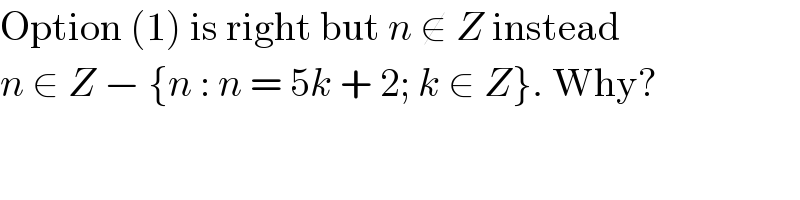
$$\mathrm{Option}\:\left(\mathrm{1}\right)\:\mathrm{is}\:\mathrm{right}\:\mathrm{but}\:{n}\:\notin\:{Z}\:\mathrm{instead} \\ $$$${n}\:\in\:{Z}\:−\:\left\{{n}\::\:{n}\:=\:\mathrm{5}{k}\:+\:\mathrm{2};\:{k}\:\in\:{Z}\right\}.\:\mathrm{Why}? \\ $$
Commented by mrW1 last updated on 27/May/17
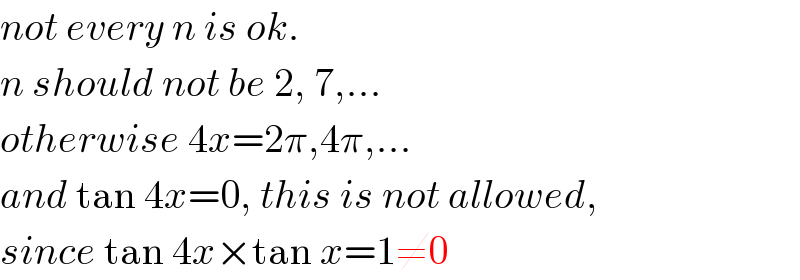
$${not}\:{every}\:{n}\:{is}\:{ok}.\: \\ $$$${n}\:{should}\:{not}\:{be}\:\mathrm{2},\:\mathrm{7},... \\ $$$${otherwise}\:\mathrm{4}{x}=\mathrm{2}\pi,\mathrm{4}\pi,... \\ $$$${and}\:\mathrm{tan}\:\mathrm{4}{x}=\mathrm{0},\:{this}\:{is}\:{not}\:{allowed}, \\ $$$${since}\:\mathrm{tan}\:\mathrm{4}{x}×\mathrm{tan}\:{x}=\mathrm{1}\neq\mathrm{0} \\ $$
Commented by Tinkutara last updated on 27/May/17

$$\mathrm{Thanks}. \\ $$
Commented by ajfour last updated on 27/May/17
![very true, and also n≠(((5m−2))/4) , m∈Z since with the definition x=(π/(10))+n(π/5) [option (1)] • tan x is never =0 • tan 5x is never zero and always not defined (which is required for tan xtan 4x =1) • tan x is not defined for two locations out of ten. • tan 4x is zero for two locations out of five first and second are good points third and fourth not so good. so we should ensure for tan x≠ undefined x=(π/(10))+n(π/5)≠kπ+(π/2) ⇒ n≠ 5k+2 , k∈ Z also for tan 4x≠ 0 4x=4((π/(10))+n(π/5))≠mπ ⇒ (2/5)+((4n)/5)≠m or n≠ ((5m−2)/4) , m ∈ Z .](Q14048.png)
$${very}\:{true},\:{and}\:{also} \\ $$$${n}\neq\frac{\left(\mathrm{5}{m}−\mathrm{2}\right)}{\mathrm{4}}\:\:,\:{m}\in{Z} \\ $$$${since}\:{with}\:{the}\:{definition} \\ $$$${x}=\frac{\pi}{\mathrm{10}}+{n}\frac{\pi}{\mathrm{5}}\:\:\:\:\:\left[{option}\:\left(\mathrm{1}\right)\right] \\ $$$$\bullet\:\:\mathrm{tan}\:{x}\:{is}\:{never}\:=\mathrm{0} \\ $$$$\bullet\:\:\mathrm{tan}\:\mathrm{5}{x}\:{is}\:{never}\:{zero}\:{and}\:{always} \\ $$$$\:\:\:\:\:{not}\:{defined}\:\left({which}\:{is}\:{required}\right. \\ $$$$\left.\:\:\:\:\:{for}\:\mathrm{tan}\:{x}\mathrm{tan}\:\mathrm{4}{x}\:=\mathrm{1}\right) \\ $$$$\bullet\:\:\:\mathrm{tan}\:{x}\:{is}\:{not}\:{defined}\:{for} \\ $$$$\:\:\:\:\:\:{two}\:{locations}\:{out}\:{of}\:{ten}. \\ $$$$\bullet\:\:\:\mathrm{tan}\:\mathrm{4}{x}\:{is}\:{zero}\:{for}\:{two}\:{locations} \\ $$$$\:\:\:\:\:\:{out}\:{of}\:{five}\: \\ $$$${first}\:{and}\:{second}\:{are}\:{good}\:{points} \\ $$$${third}\:{and}\:{fourth}\:{not}\:{so}\:{good}. \\ $$$$\mathrm{so}\:\:\mathrm{we}\:\mathrm{should}\:\mathrm{ensure} \\ $$$$\:\:\:{for}\:\mathrm{tan}\:{x}\neq\:{undefined}\: \\ $$$$\:\:\:{x}=\frac{\pi}{\mathrm{10}}+{n}\frac{\pi}{\mathrm{5}}\neq{k}\pi+\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:{n}\neq\:\mathrm{5}{k}+\mathrm{2}\:,\:\:{k}\in\:{Z} \\ $$$$\:\:{also}\:{for}\:\:\:\mathrm{tan}\:\mathrm{4}{x}\neq\:\mathrm{0} \\ $$$$\mathrm{4}{x}=\mathrm{4}\left(\frac{\pi}{\mathrm{10}}+{n}\frac{\pi}{\mathrm{5}}\right)\neq{m}\pi \\ $$$$\Rightarrow\:\:\frac{\mathrm{2}}{\mathrm{5}}+\frac{\mathrm{4}{n}}{\mathrm{5}}\neq{m}\: \\ $$$${or}\:\:\:{n}\neq\:\frac{\mathrm{5}{m}−\mathrm{2}}{\mathrm{4}}\:,\:\:{m}\:\in\:{Z}\:\:. \\ $$
Commented by Tinkutara last updated on 27/May/17

$$\mathrm{Thanks}. \\ $$
