
Question Number 86499 by ram roop sharma last updated on 29/Mar/20
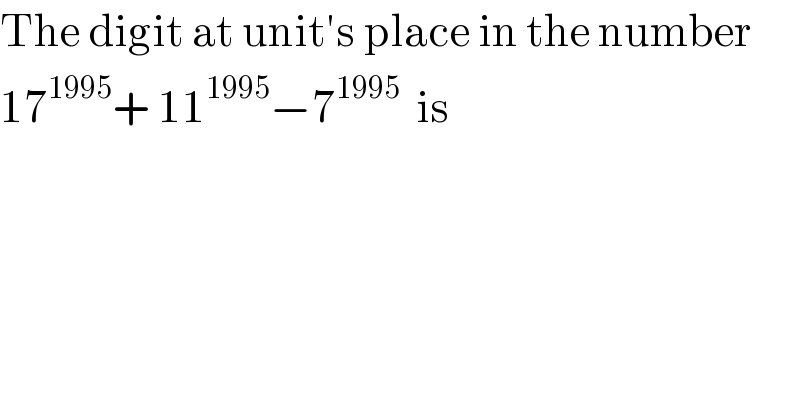
$$\mathrm{The}\:\mathrm{digit}\:\mathrm{at}\:\mathrm{unit}'\mathrm{s}\:\mathrm{place}\:\mathrm{in}\:\mathrm{the}\:\mathrm{number} \\ $$$$\mathrm{17}^{\mathrm{1995}} +\:\mathrm{11}^{\mathrm{1995}} −\mathrm{7}^{\mathrm{1995}} \:\:\mathrm{is} \\ $$
Commented by Serlea last updated on 29/Mar/20
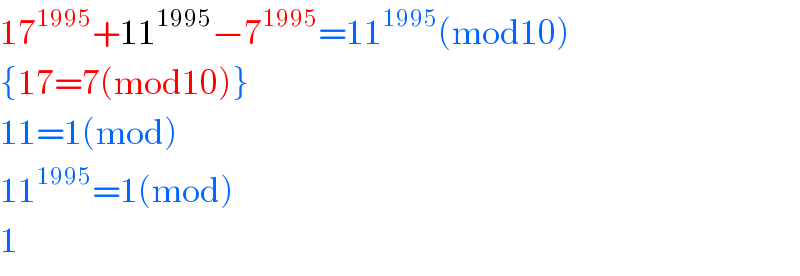
$$\mathrm{17}^{\mathrm{1995}} +\mathrm{11}^{\mathrm{1995}} −\mathrm{7}^{\mathrm{1995}} =\mathrm{11}^{\mathrm{1995}} \left(\mathrm{mod10}\right) \\ $$$$\left\{\mathrm{17}=\mathrm{7}\left(\mathrm{mod10}\right)\right\} \\ $$$$\mathrm{11}=\mathrm{1}\left(\mathrm{mod}\right) \\ $$$$\mathrm{11}^{\mathrm{1995}} =\mathrm{1}\left(\mathrm{mod}\right) \\ $$$$\mathrm{1} \\ $$
Answered by redmiiuser last updated on 29/Mar/20

$$\mathrm{1} \\ $$$${as}\:{we}\:{know}\:{that}\:{the} \\ $$$${unit}\:{digit}\:{of}\:\mathrm{17}^{\mathrm{5}} \:{and}\:\mathrm{7}^{\mathrm{5}} \:{and}\:\mathrm{7} \\ $$$${and}\:{that}\:{of}\:\mathrm{11}^{\mathrm{5}} \:{is}\:\mathrm{1} \\ $$$${so}\:{same}\:{with}\:\mathrm{17}^{\mathrm{1995}} \:,\mathrm{7}^{\mathrm{1995}} \\ $$$${and}\:\mathrm{11}^{\mathrm{1995}} \:{the}\:{unit}\:{digits} \\ $$$${are}\:\mathrm{7}\:{and}\:\mathrm{1}. \\ $$$${now}\:\mathrm{7}+\mathrm{1}−\mathrm{7}=\mathrm{1} \\ $$$$ \\ $$
