
Question Number 176098 by nadovic last updated on 12/Sep/22

$$\mathrm{The}\:\mathrm{deviations}\:\mathrm{of}\:\mathrm{a}\:\mathrm{set}\:\mathrm{of}\:\mathrm{numbers} \\ $$$$\mathrm{from}\:\mathrm{12}\:\mathrm{are}\: \\ $$$$\:\:\:\:\:\mathrm{3},\:−\mathrm{2},\:\mathrm{1},\:\mathrm{0},\:−\mathrm{1},\:\mathrm{4},\:\mathrm{0},\:\mathrm{1}\:\mathrm{and}\:\mathrm{2}. \\ $$$$\mathrm{Calculate}\:\mathrm{the}\:\mathrm{mean}\:\mathrm{and}\:\mathrm{standard}\: \\ $$$$\mathrm{deviation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{numbers}. \\ $$
Answered by Rasheed.Sindhi last updated on 12/Sep/22
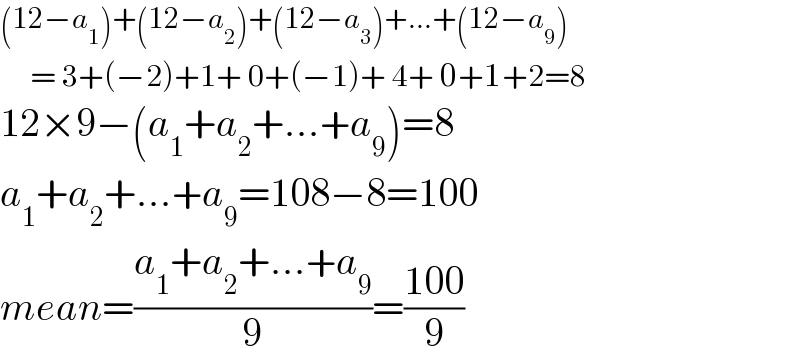
$$\left(\mathrm{12}−{a}_{\mathrm{1}} \right)+\left(\mathrm{12}−{a}_{\mathrm{2}} \right)+\left(\mathrm{12}−{a}_{\mathrm{3}} \right)+...+\left(\mathrm{12}−{a}_{\mathrm{9}} \right) \\ $$$$\:\:\:\:\:=\:\mathrm{3}+\left(−\mathrm{2}\right)+\mathrm{1}+\:\mathrm{0}+\left(−\mathrm{1}\right)+\:\mathrm{4}+\:\mathrm{0}+\mathrm{1}+\mathrm{2}=\mathrm{8} \\ $$$$\mathrm{12}×\mathrm{9}−\left({a}_{\mathrm{1}} +{a}_{\mathrm{2}} +...+{a}_{\mathrm{9}} \right)=\mathrm{8} \\ $$$${a}_{\mathrm{1}} +{a}_{\mathrm{2}} +...+{a}_{\mathrm{9}} =\mathrm{108}−\mathrm{8}=\mathrm{100} \\ $$$${mean}=\frac{{a}_{\mathrm{1}} +{a}_{\mathrm{2}} +...+{a}_{\mathrm{9}} }{\mathrm{9}}=\frac{\mathrm{100}}{\mathrm{9}} \\ $$
Commented by peter frank last updated on 12/Sep/22

$$\mathrm{thanks} \\ $$
Commented by Rasheed.Sindhi last updated on 12/Sep/22
$$\mathrm{thanks}\:\mathrm{for}\:\mathrm{thanks}! \\ $$
