
Question Number 56749 by pete last updated on 22/Mar/19
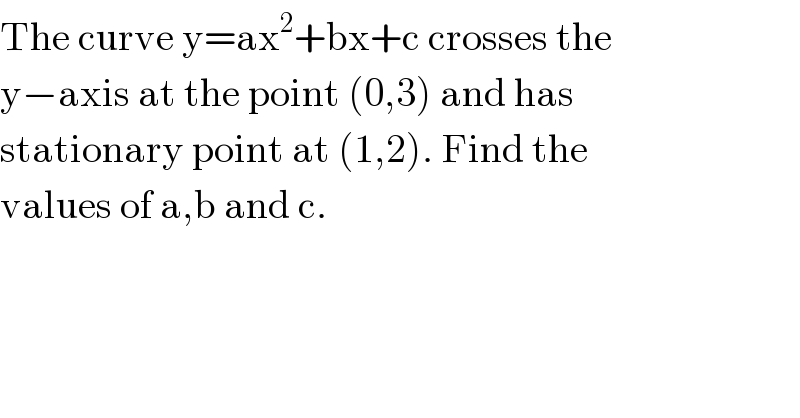
$$\mathrm{The}\:\mathrm{curve}\:\mathrm{y}=\mathrm{ax}^{\mathrm{2}} +\mathrm{bx}+\mathrm{c}\:\mathrm{crosses}\:\mathrm{the} \\ $$$$\mathrm{y}−\mathrm{axis}\:\mathrm{at}\:\mathrm{the}\:\mathrm{point}\:\left(\mathrm{0},\mathrm{3}\right)\:\mathrm{and}\:\mathrm{has} \\ $$$$\mathrm{stationary}\:\mathrm{point}\:\mathrm{at}\:\left(\mathrm{1},\mathrm{2}\right).\:\mathrm{Find}\:\mathrm{the} \\ $$$$\mathrm{values}\:\mathrm{of}\:\mathrm{a},\mathrm{b}\:\mathrm{and}\:\mathrm{c}. \\ $$
Answered by ajfour last updated on 22/Mar/19

$$\mathrm{c}=\mathrm{3} \\ $$$$\mathrm{2a}\left(\mathrm{1}\right)+\mathrm{b}=\mathrm{0} \\ $$$$\mathrm{2}=\mathrm{a}+\mathrm{b}+\mathrm{3} \\ $$$$\Rightarrow\mathrm{2a}+\mathrm{2}=\mathrm{a}+\mathrm{3}\:\:\:\Rightarrow\:\:\mathrm{a}=\mathrm{1} \\ $$$$\mathrm{and}\:\mathrm{b}=−\mathrm{2}\:. \\ $$$$\:\:\mathrm{y}=\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{3}\:. \\ $$
