
Question Number 63937 by gunawan last updated on 11/Jul/19
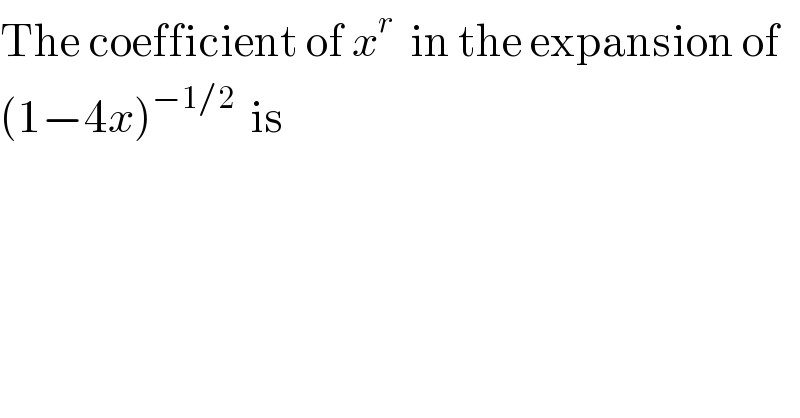
$$\mathrm{The}\:\mathrm{coefficient}\:\mathrm{of}\:{x}^{{r}} \:\:\mathrm{in}\:\mathrm{the}\:\mathrm{expansion}\:\mathrm{of} \\ $$$$\left(\mathrm{1}−\mathrm{4}{x}\right)^{−\mathrm{1}/\mathrm{2}} \:\:\mathrm{is} \\ $$
Answered by mr W last updated on 12/Jul/19
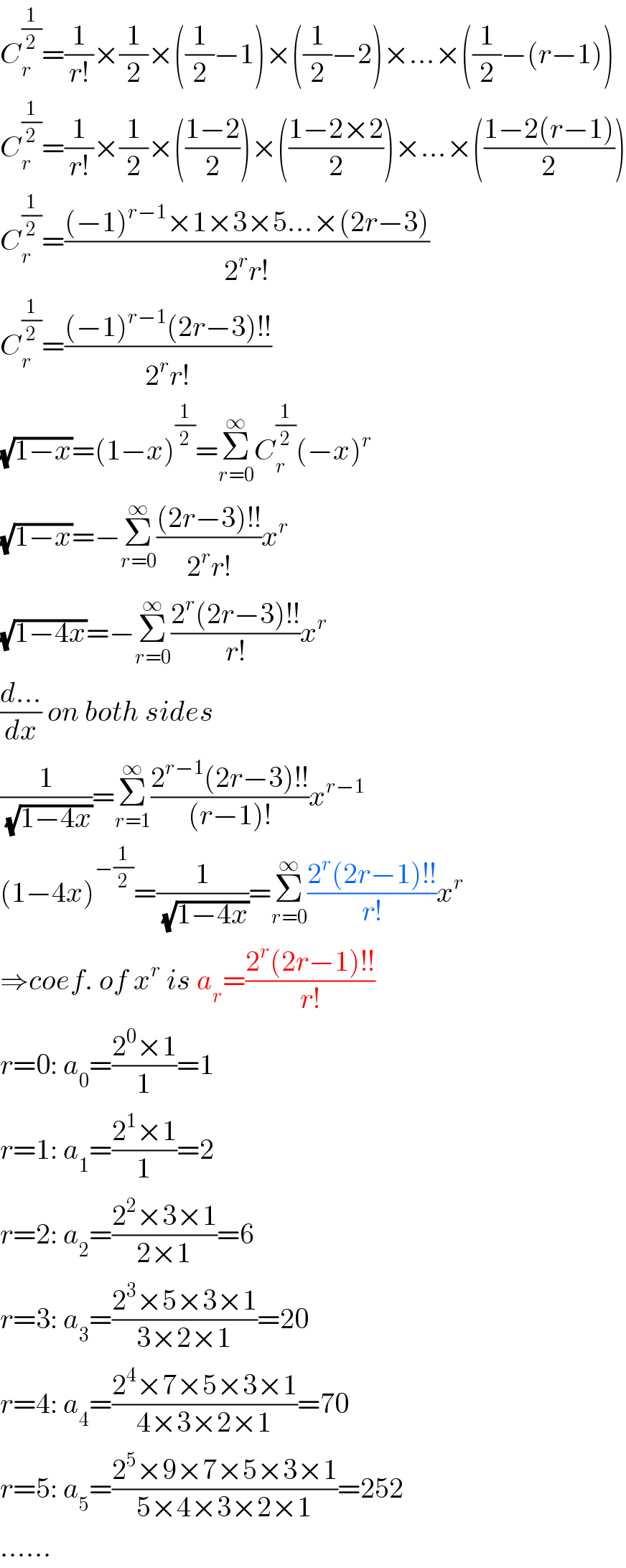
$${C}_{{r}} ^{\frac{\mathrm{1}}{\mathrm{2}}} =\frac{\mathrm{1}}{{r}!}×\frac{\mathrm{1}}{\mathrm{2}}×\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)×\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}\right)×...×\left(\frac{\mathrm{1}}{\mathrm{2}}−\left({r}−\mathrm{1}\right)\right) \\ $$$${C}_{{r}} ^{\frac{\mathrm{1}}{\mathrm{2}}} =\frac{\mathrm{1}}{{r}!}×\frac{\mathrm{1}}{\mathrm{2}}×\left(\frac{\mathrm{1}−\mathrm{2}}{\mathrm{2}}\right)×\left(\frac{\mathrm{1}−\mathrm{2}×\mathrm{2}}{\mathrm{2}}\right)×...×\left(\frac{\mathrm{1}−\mathrm{2}\left({r}−\mathrm{1}\right)}{\mathrm{2}}\right) \\ $$$${C}_{{r}} ^{\frac{\mathrm{1}}{\mathrm{2}}} =\frac{\left(−\mathrm{1}\right)^{{r}−\mathrm{1}} ×\mathrm{1}×\mathrm{3}×\mathrm{5}...×\left(\mathrm{2}{r}−\mathrm{3}\right)}{\mathrm{2}^{{r}} {r}!} \\ $$$${C}_{{r}} ^{\frac{\mathrm{1}}{\mathrm{2}}} =\frac{\left(−\mathrm{1}\right)^{{r}−\mathrm{1}} \left(\mathrm{2}{r}−\mathrm{3}\right)!!}{\mathrm{2}^{{r}} {r}!} \\ $$$$\sqrt{\mathrm{1}−{x}}=\left(\mathrm{1}−{x}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}{C}_{{r}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \left(−{x}\right)^{{r}} \\ $$$$\sqrt{\mathrm{1}−{x}}=−\underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{2}{r}−\mathrm{3}\right)!!}{\mathrm{2}^{{r}} {r}!}{x}^{{r}} \\ $$$$\sqrt{\mathrm{1}−\mathrm{4}{x}}=−\underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2}^{{r}} \left(\mathrm{2}{r}−\mathrm{3}\right)!!}{{r}!}{x}^{{r}} \\ $$$$\frac{{d}...}{{dx}}\:{on}\:{both}\:{sides} \\ $$$$\frac{\mathrm{1}}{\sqrt{\mathrm{1}−\mathrm{4}{x}}}=\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}^{{r}−\mathrm{1}} \left(\mathrm{2}{r}−\mathrm{3}\right)!!}{\left({r}−\mathrm{1}\right)!}{x}^{{r}−\mathrm{1}} \\ $$$$\left(\mathrm{1}−\mathrm{4}{x}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} =\frac{\mathrm{1}}{\sqrt{\mathrm{1}−\mathrm{4}{x}}}=\underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2}^{{r}} \left(\mathrm{2}{r}−\mathrm{1}\right)!!}{{r}!}{x}^{{r}} \\ $$$$\Rightarrow{coef}.\:{of}\:{x}^{{r}} \:{is}\:{a}_{{r}} =\frac{\mathrm{2}^{{r}} \left(\mathrm{2}{r}−\mathrm{1}\right)!!}{{r}!} \\ $$$${r}=\mathrm{0}:\:{a}_{\mathrm{0}} =\frac{\mathrm{2}^{\mathrm{0}} ×\mathrm{1}}{\mathrm{1}}=\mathrm{1} \\ $$$${r}=\mathrm{1}:\:{a}_{\mathrm{1}} =\frac{\mathrm{2}^{\mathrm{1}} ×\mathrm{1}}{\mathrm{1}}=\mathrm{2} \\ $$$${r}=\mathrm{2}:\:{a}_{\mathrm{2}} =\frac{\mathrm{2}^{\mathrm{2}} ×\mathrm{3}×\mathrm{1}}{\mathrm{2}×\mathrm{1}}=\mathrm{6} \\ $$$${r}=\mathrm{3}:\:{a}_{\mathrm{3}} =\frac{\mathrm{2}^{\mathrm{3}} ×\mathrm{5}×\mathrm{3}×\mathrm{1}}{\mathrm{3}×\mathrm{2}×\mathrm{1}}=\mathrm{20} \\ $$$${r}=\mathrm{4}:\:{a}_{\mathrm{4}} =\frac{\mathrm{2}^{\mathrm{4}} ×\mathrm{7}×\mathrm{5}×\mathrm{3}×\mathrm{1}}{\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{1}}=\mathrm{70} \\ $$$${r}=\mathrm{5}:\:{a}_{\mathrm{5}} =\frac{\mathrm{2}^{\mathrm{5}} ×\mathrm{9}×\mathrm{7}×\mathrm{5}×\mathrm{3}×\mathrm{1}}{\mathrm{5}×\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{1}}=\mathrm{252} \\ $$$$...... \\ $$
