
Question Number 32543 by rahul 19 last updated on 27/Mar/18
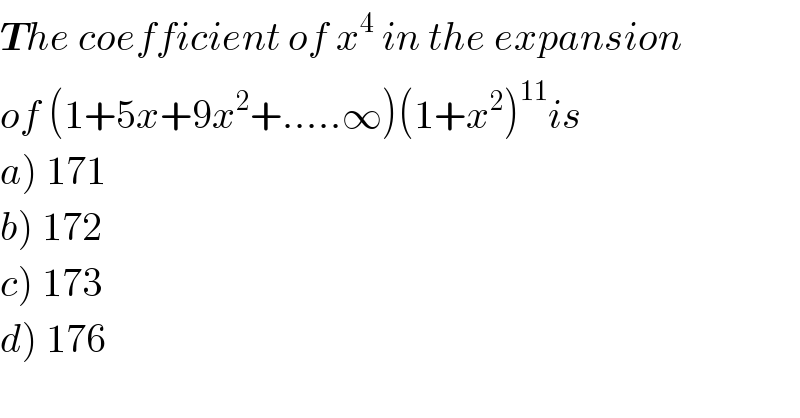
$$\boldsymbol{{T}}{he}\:{coefficient}\:{of}\:{x}^{\mathrm{4}} \:{in}\:{the}\:{expansion} \\ $$$${of}\:\left(\mathrm{1}+\mathrm{5}{x}+\mathrm{9}{x}^{\mathrm{2}} +.....\infty\right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{11}} {is} \\ $$$$\left.{a}\right)\:\mathrm{171} \\ $$$$\left.{b}\right)\:\mathrm{172} \\ $$$$\left.{c}\right)\:\mathrm{173} \\ $$$$\left.{d}\right)\:\mathrm{176} \\ $$
Answered by mrW2 last updated on 27/Mar/18
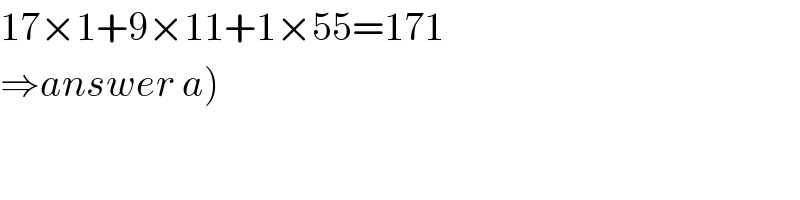
$$\mathrm{17}×\mathrm{1}+\mathrm{9}×\mathrm{11}+\mathrm{1}×\mathrm{55}=\mathrm{171} \\ $$$$\left.\Rightarrow{answer}\:{a}\right) \\ $$
Commented by rahul 19 last updated on 27/Mar/18

$${thank}\:{u}\:{both}! \\ $$
Commented by MJS last updated on 27/Mar/18
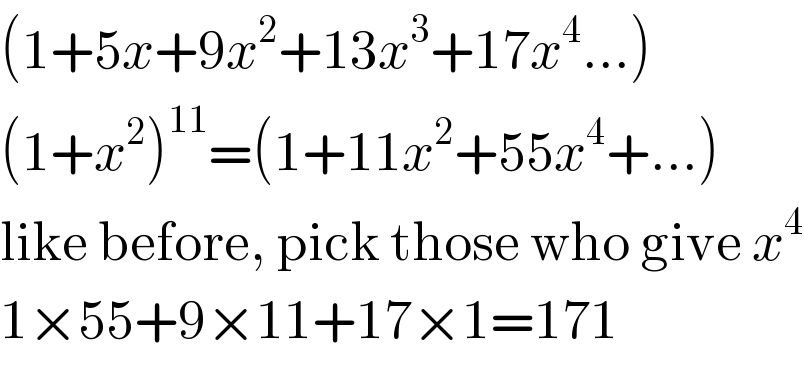
$$\left(\mathrm{1}+\mathrm{5}{x}+\mathrm{9}{x}^{\mathrm{2}} +\mathrm{13}{x}^{\mathrm{3}} +\mathrm{17}{x}^{\mathrm{4}} ...\right) \\ $$$$\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{11}} =\left(\mathrm{1}+\mathrm{11}{x}^{\mathrm{2}} +\mathrm{55}{x}^{\mathrm{4}} +...\right) \\ $$$$\mathrm{like}\:\mathrm{before},\:\mathrm{pick}\:\mathrm{those}\:\mathrm{who}\:\mathrm{give}\:{x}^{\mathrm{4}} \\ $$$$\mathrm{1}×\mathrm{55}+\mathrm{9}×\mathrm{11}+\mathrm{17}×\mathrm{1}=\mathrm{171} \\ $$
