Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 177507 by peter frank last updated on 06/Oct/22

The angle of elevetion of the top of a tower from a point A in the north is α and the angle of the top of the tower from the point B in the east of the point A is β .prove that the height of the tower is ((ABsin αsin B)/( (√(sin^2 α−sin^2 β))))

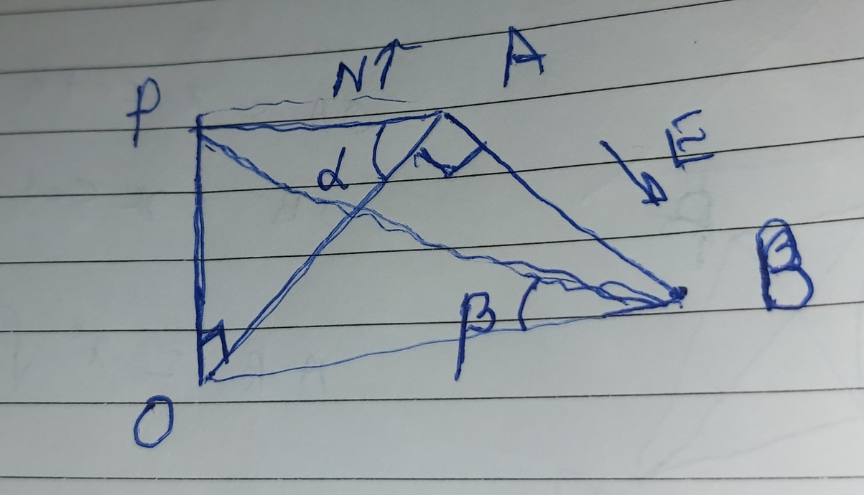
$$\mathrm{The}\:\mathrm{angle}\:\mathrm{of}\:\mathrm{elevetion}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{top}\:\mathrm{of}\:\mathrm{a}\:\mathrm{tower}\:\mathrm{from}\:\mathrm{a}\:\mathrm{point}\: \\ $$$$\mathrm{A}\:\mathrm{in}\:\mathrm{the}\:\mathrm{north}\:\mathrm{is}\:\alpha\:\mathrm{and}\:\mathrm{the}\: \\ $$$$\mathrm{angle}\:\mathrm{of}\:\mathrm{the}\:\mathrm{top}\:\mathrm{of}\:\mathrm{the}\:\mathrm{tower} \\ $$$$\mathrm{from}\:\mathrm{the}\:\mathrm{point}\:\mathrm{B}\:\mathrm{in}\:\mathrm{the}\:\mathrm{east}\:\mathrm{of}\:\mathrm{the}\:\mathrm{point} \\ $$$$\mathrm{A}\:\mathrm{is}\:\beta\:.\mathrm{prove}\:\mathrm{that}\:\mathrm{the}\:\mathrm{height} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{tower}\:\mathrm{is}\: \\ $$$$\frac{\mathrm{ABsin}\:\alpha\mathrm{sin}\:\mathrm{B}}{\:\sqrt{\mathrm{sin}\:^{\mathrm{2}} \alpha−\mathrm{sin}\:^{\mathrm{2}} \beta}} \\ $$

Answered by som(math1967) last updated on 06/Oct/22

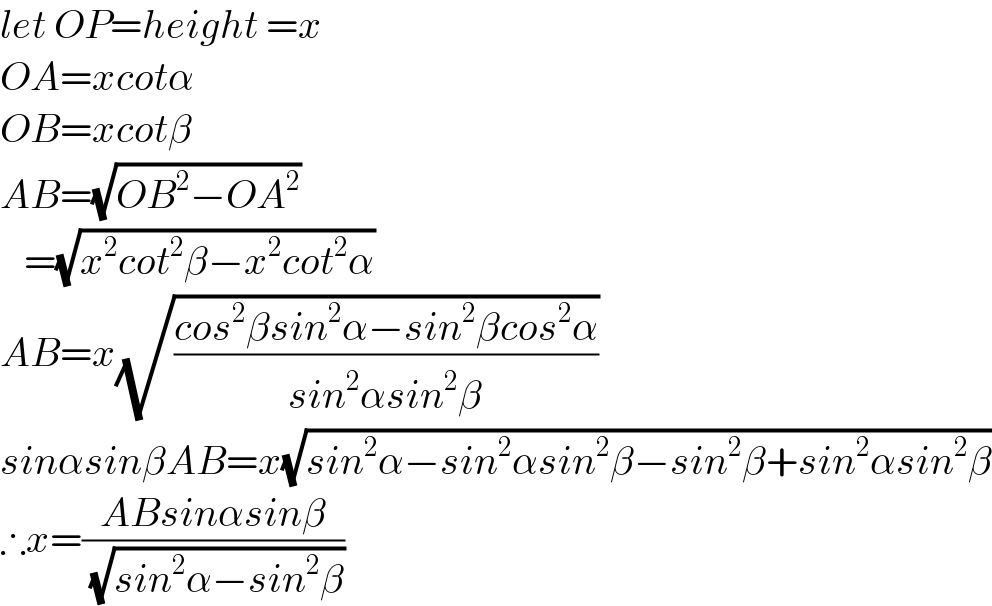
let OP=height =x OA=xcotα OB=xcotβ AB=(√(OB^2 −OA^2 )) =(√(x^2 cot^2 β−x^2 cot^2 α)) AB=x(√((cos^2 βsin^2 α−sin^2 βcos^2 α)/(sin^2 αsin^2 β))) sinαsinβAB=x(√(sin^2 α−sin^2 αsin^2 β−sin^2 β+sin^2 αsin^2 β)) ∴x=((ABsinαsinβ)/( (√(sin^2 α−sin^2 β))))

$${let}\:{OP}={height}\:={x} \\ $$$${OA}={xcot}\alpha \\ $$$${OB}={xcot}\beta \\ $$$${AB}=\sqrt{{OB}^{\mathrm{2}} −{OA}^{\mathrm{2}} } \\ $$$$\:\:\:=\sqrt{{x}^{\mathrm{2}} {cot}^{\mathrm{2}} \beta−{x}^{\mathrm{2}} {cot}^{\mathrm{2}} \alpha} \\ $$$${AB}={x}\sqrt{\frac{{cos}^{\mathrm{2}} \beta{sin}^{\mathrm{2}} \alpha−{sin}^{\mathrm{2}} \beta{cos}^{\mathrm{2}} \alpha}{{sin}^{\mathrm{2}} \alpha{sin}^{\mathrm{2}} \beta}} \\ $$$${sin}\alpha{sin}\beta{AB}={x}\sqrt{{sin}^{\mathrm{2}} \alpha−{sin}^{\mathrm{2}} \alpha{sin}^{\mathrm{2}} \beta−{sin}^{\mathrm{2}} \beta+{sin}^{\mathrm{2}} \alpha{sin}^{\mathrm{2}} \beta} \\ $$$$\therefore{x}=\frac{{ABsin}\alpha{sin}\beta}{\:\sqrt{{sin}^{\mathrm{2}} \alpha−{sin}^{\mathrm{2}} \beta}} \\ $$

Commented by som(math1967) last updated on 06/Oct/22

Commented by peter frank last updated on 06/Oct/22

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com