Question and Answers Forum

All Questions      Topic List

Permutation and Combination Questions

Previous in All Question      Next in All Question      

Previous in Permutation and Combination      Next in Permutation and Combination      

Question Number 54646 by gunawan last updated on 08/Feb/19

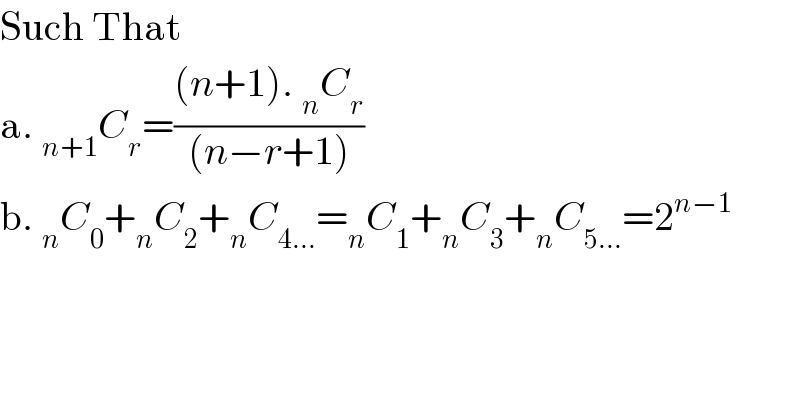
Such That a. _(n+1) C_r =(((n+1). _n C_r )/((n−r+1))) b. _n C_0 +_n C_2 +_n C_(4...) =_n C_1 +_n C_3 +_n C_(5...) =2^(n−1)

$$\mathrm{Such}\:\mathrm{That} \\ $$$$\mathrm{a}.\:_{{n}+\mathrm{1}} {C}_{{r}} =\frac{\left({n}+\mathrm{1}\right).\:_{{n}} {C}_{{r}} }{\left({n}−{r}+\mathrm{1}\right)} \\ $$$$\mathrm{b}.\:_{{n}} {C}_{\mathrm{0}} +_{{n}} {C}_{\mathrm{2}} +_{{n}} {C}_{\mathrm{4}...} =_{{n}} {C}_{\mathrm{1}} +_{{n}} {C}_{\mathrm{3}} +_{{n}} {C}_{\mathrm{5}...} =\mathrm{2}^{{n}−\mathrm{1}} \\ $$$$ \\ $$

Answered by Kunal12588 last updated on 08/Feb/19

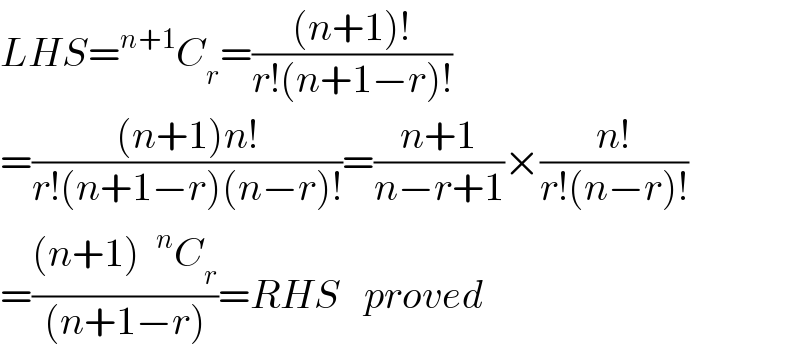
LHS=^(n+1) C_r =(((n+1)!)/(r!(n+1−r)!)) =(((n+1)n!)/(r!(n+1−r)(n−r)!))=((n+1)/(n−r+1))×((n!)/(r!(n−r)!)) =(((n+1) ^n C_r )/((n+1−r)))=RHS proved

$${LHS}=^{{n}+\mathrm{1}} {C}_{{r}} =\frac{\left({n}+\mathrm{1}\right)!}{{r}!\left({n}+\mathrm{1}−{r}\right)!} \\ $$$$=\frac{\left({n}+\mathrm{1}\right){n}!}{{r}!\left({n}+\mathrm{1}−{r}\right)\left({n}−{r}\right)!}=\frac{{n}+\mathrm{1}}{{n}−{r}+\mathrm{1}}×\frac{{n}!}{{r}!\left({n}−{r}\right)!} \\ $$$$=\frac{\left({n}+\mathrm{1}\right)\:\:^{{n}} {C}_{{r}} }{\left({n}+\mathrm{1}−{r}\right)}={RHS}\:\:\:{proved} \\ $$

Commented by gunawan last updated on 08/Feb/19

thank you Sir

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{Sir} \\ $$

Answered by Kunal12588 last updated on 10/Feb/19

b. from binimial expansion 0^n =(1−1)^n ⇒0=^n C_0 −^n C_1 +^n C_2 −.....+(−1)^n ∙^n C_n ⇒^n C_0 +^n C_2 +^n C_4 +....=^n C_1 +^n C_3 +^n C_5 +.... eq(1) LHS of eq(1) ^n C_0 +^n C_2 +^n C_4 +.... =^(n−1) C_0 +^(n−1) C_1 +^(n−1) C_2 +^(n−1) C_3 +^(n−1) C_4 +... =2^(n−1) proved I used the identities (1) and (3) from question 54740 see carefully

$${b}.\:\:{from}\:{binimial}\:{expansion} \\ $$$$\mathrm{0}^{{n}} =\left(\mathrm{1}−\mathrm{1}\right)^{{n}} \\ $$$$\Rightarrow\mathrm{0}=^{{n}} {C}_{\mathrm{0}} −^{{n}} {C}_{\mathrm{1}} +^{{n}} {C}_{\mathrm{2}} −.....+\left(−\mathrm{1}\right)^{{n}} \:\centerdot\:^{{n}} {C}_{{n}} \\ $$$$\Rightarrow^{{n}} {C}_{\mathrm{0}} +^{{n}} {C}_{\mathrm{2}} +^{{n}} {C}_{\mathrm{4}} +....=^{{n}} {C}_{\mathrm{1}} +^{{n}} {C}_{\mathrm{3}} +^{{n}} {C}_{\mathrm{5}} +....\:\:\:\:{eq}\left(\mathrm{1}\right) \\ $$$${LHS}\:\:{of}\:{eq}\left(\mathrm{1}\right) \\ $$$$\:^{{n}} {C}_{\mathrm{0}} +^{{n}} {C}_{\mathrm{2}} +^{{n}} {C}_{\mathrm{4}} +.... \\ $$$$=^{{n}−\mathrm{1}} {C}_{\mathrm{0}} +^{{n}−\mathrm{1}} {C}_{\mathrm{1}} +^{{n}−\mathrm{1}} {C}_{\mathrm{2}} +^{{n}−\mathrm{1}} {C}_{\mathrm{3}} +^{{n}−\mathrm{1}} {C}_{\mathrm{4}} +... \\ $$$$=\mathrm{2}^{{n}−\mathrm{1}} \:\:\:\:{proved} \\ $$$${I}\:{used}\:{the}\:{identities}\:\left(\mathrm{1}\right)\:{and}\:\left(\mathrm{3}\right)\:\:{from}\: \\ $$$${question}\:\mathrm{54740}\:{see}\:{carefully} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com