
Question Number 12442 by tawa last updated on 22/Apr/17

$$\mathrm{Solve}:\:\:\:\mathrm{z}^{\mathrm{4}} \:=\:−\:\mathrm{16} \\ $$
Answered by ajfour last updated on 22/Apr/17
![z^4 =2^4 e^(i(π+2kπ)) z=2e^(i((π/4)+((2kπ)/4) )) ∀ k=0,1,−1,−2 so z_1 =2[cos (π/4)+isin (π/4)] z_2 =2[cos (3π/4)+isin (3π/4)] z_3 =2[cos (−π/4)+isin (−π/4)] z_4 =2[cos (−3π/4)+isin (−3π/4)] to summarize z=(√2)(±1±i) .](Q12447.png)
$${z}^{\mathrm{4}} =\mathrm{2}^{\mathrm{4}} {e}^{{i}\left(\pi+\mathrm{2}{k}\pi\right)} \\ $$$${z}=\mathrm{2}{e}^{{i}\left(\frac{\pi}{\mathrm{4}}+\frac{\mathrm{2}{k}\pi}{\mathrm{4}}\:\right)} \:\:\:\:\:\:\forall\:{k}=\mathrm{0},\mathrm{1},−\mathrm{1},−\mathrm{2} \\ $$$${so}\:{z}_{\mathrm{1}} =\mathrm{2}\left[\mathrm{cos}\:\left(\pi/\mathrm{4}\right)+{i}\mathrm{sin}\:\left(\pi/\mathrm{4}\right)\right] \\ $$$${z}_{\mathrm{2}} =\mathrm{2}\left[\mathrm{cos}\:\left(\mathrm{3}\pi/\mathrm{4}\right)+{i}\mathrm{sin}\:\left(\mathrm{3}\pi/\mathrm{4}\right)\right] \\ $$$${z}_{\mathrm{3}} =\mathrm{2}\left[\mathrm{cos}\:\left(−\pi/\mathrm{4}\right)+{i}\mathrm{sin}\:\left(−\pi/\mathrm{4}\right)\right] \\ $$$${z}_{\mathrm{4}} =\mathrm{2}\left[\mathrm{cos}\:\left(−\mathrm{3}\pi/\mathrm{4}\right)+{i}\mathrm{sin}\:\left(−\mathrm{3}\pi/\mathrm{4}\right)\right] \\ $$$${to}\:{summarize} \\ $$$${z}=\sqrt{\mathrm{2}}\left(\pm\mathrm{1}\pm{i}\right)\:. \\ $$
Commented by tawa last updated on 22/Apr/17

$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
Answered by mrW1 last updated on 23/Apr/17
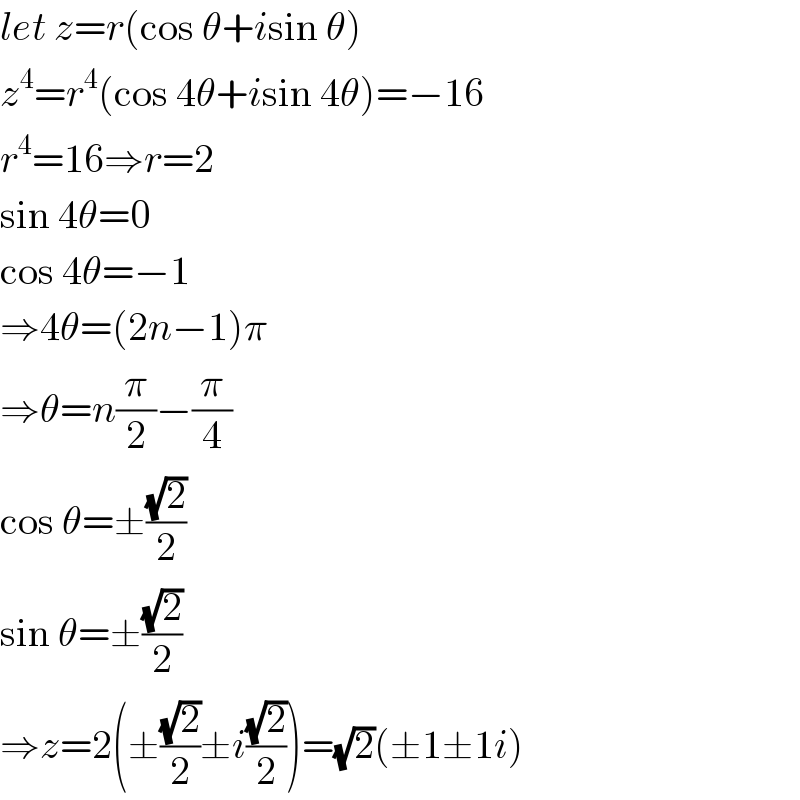
$${let}\:{z}={r}\left(\mathrm{cos}\:\theta+{i}\mathrm{sin}\:\theta\right) \\ $$$${z}^{\mathrm{4}} ={r}^{\mathrm{4}} \left(\mathrm{cos}\:\mathrm{4}\theta+{i}\mathrm{sin}\:\mathrm{4}\theta\right)=−\mathrm{16} \\ $$$${r}^{\mathrm{4}} =\mathrm{16}\Rightarrow{r}=\mathrm{2} \\ $$$$\mathrm{sin}\:\mathrm{4}\theta=\mathrm{0} \\ $$$$\mathrm{cos}\:\mathrm{4}\theta=−\mathrm{1} \\ $$$$\Rightarrow\mathrm{4}\theta=\left(\mathrm{2}{n}−\mathrm{1}\right)\pi \\ $$$$\Rightarrow\theta={n}\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{4}} \\ $$$$\mathrm{cos}\:\theta=\pm\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\mathrm{sin}\:\theta=\pm\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\Rightarrow{z}=\mathrm{2}\left(\pm\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\pm{i}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)=\sqrt{\mathrm{2}}\left(\pm\mathrm{1}\pm\mathrm{1}{i}\right) \\ $$
Commented by tawa last updated on 23/Apr/17

$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
