Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 40422 by rahul 19 last updated on 21/Jul/18

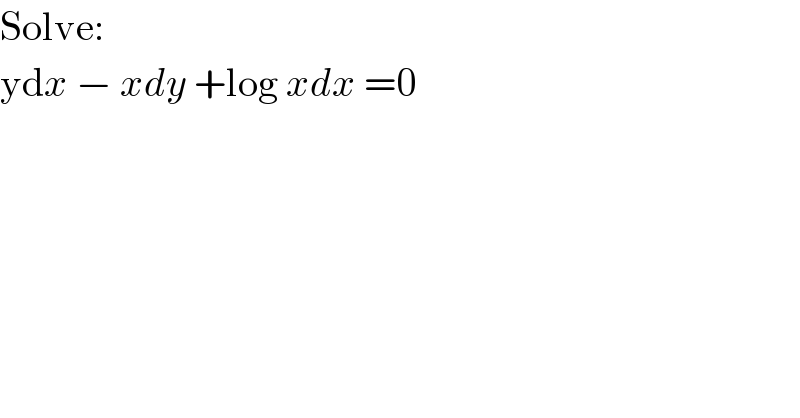
Solve: ydx − xdy +log xdx =0

$$\mathrm{Solve}: \\ $$$$\mathrm{yd}{x}\:−\:{xdy}\:+\mathrm{log}\:{xdx}\:=\mathrm{0} \\ $$

Commented by prof Abdo imad last updated on 22/Jul/18

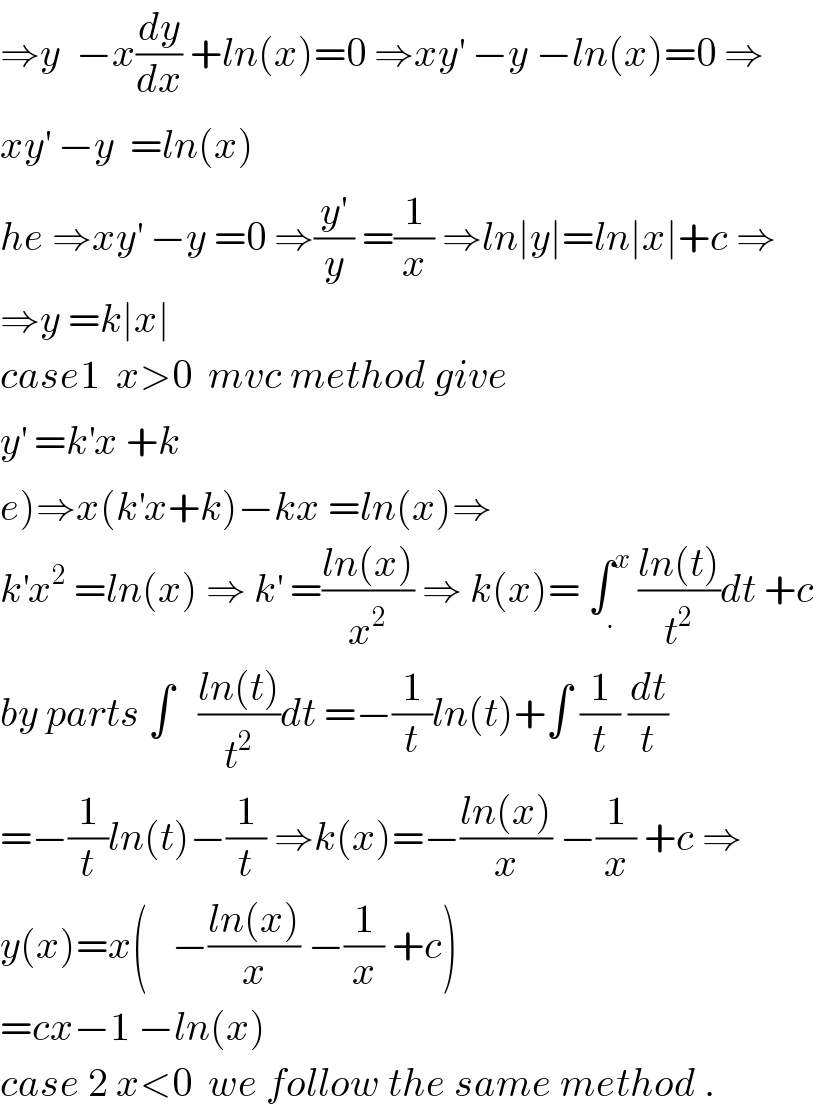
⇒y −x(dy/dx) +ln(x)=0 ⇒xy^′ −y −ln(x)=0 ⇒ xy^′ −y =ln(x) he ⇒xy^′ −y =0 ⇒(y^′ /y) =(1/x) ⇒ln∣y∣=ln∣x∣+c ⇒ ⇒y =k∣x∣ case1 x>0 mvc method give y^′ =k^′ x +k e)⇒x(k^′ x+k)−kx =ln(x)⇒ k^′ x^2 =ln(x) ⇒ k^′ =((ln(x))/x^2 ) ⇒ k(x)= ∫_. ^x ((ln(t))/t^2 )dt +c by parts ∫ ((ln(t))/t^2 )dt =−(1/t)ln(t)+∫ (1/t) (dt/t) =−(1/t)ln(t)−(1/t) ⇒k(x)=−((ln(x))/x) −(1/x) +c ⇒ y(x)=x( −((ln(x))/x) −(1/x) +c) =cx−1 −ln(x) case 2 x<0 we follow the same method .

$$\Rightarrow{y}\:\:−{x}\frac{{dy}}{{dx}}\:+{ln}\left({x}\right)=\mathrm{0}\:\Rightarrow{xy}^{'} \:−{y}\:−{ln}\left({x}\right)=\mathrm{0}\:\Rightarrow \\ $$$${xy}^{'} \:−{y}\:\:={ln}\left({x}\right)\:\: \\ $$$${he}\:\Rightarrow{xy}^{'} \:−{y}\:=\mathrm{0}\:\Rightarrow\frac{{y}^{'} }{{y}}\:=\frac{\mathrm{1}}{{x}}\:\Rightarrow{ln}\mid{y}\mid={ln}\mid{x}\mid+{c}\:\Rightarrow \\ $$$$\Rightarrow{y}\:={k}\mid{x}\mid\: \\ $$$${case}\mathrm{1}\:\:{x}>\mathrm{0}\:\:{mvc}\:{method}\:{give}\: \\ $$$${y}^{'} \:={k}^{'} {x}\:+{k} \\ $$$$\left.{e}\right)\Rightarrow{x}\left({k}^{'} {x}+{k}\right)−{kx}\:={ln}\left({x}\right)\Rightarrow \\ $$$${k}^{'} {x}^{\mathrm{2}} \:={ln}\left({x}\right)\:\Rightarrow\:{k}^{'} \:=\frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} }\:\Rightarrow\:{k}\left({x}\right)=\:\int_{.} ^{{x}} \:\frac{{ln}\left({t}\right)}{{t}^{\mathrm{2}} }{dt}\:+{c} \\ $$$${by}\:{parts}\:\int\:\:\:\frac{{ln}\left({t}\right)}{{t}^{\mathrm{2}} }{dt}\:=−\frac{\mathrm{1}}{{t}}{ln}\left({t}\right)+\int\:\frac{\mathrm{1}}{{t}}\:\frac{{dt}}{{t}} \\ $$$$=−\frac{\mathrm{1}}{{t}}{ln}\left({t}\right)−\frac{\mathrm{1}}{{t}}\:\Rightarrow{k}\left({x}\right)=−\frac{{ln}\left({x}\right)}{{x}}\:−\frac{\mathrm{1}}{{x}}\:+{c}\:\Rightarrow \\ $$$${y}\left({x}\right)={x}\left(\:\:\:−\frac{{ln}\left({x}\right)}{{x}}\:−\frac{\mathrm{1}}{{x}}\:+{c}\right) \\ $$$$={cx}−\mathrm{1}\:−{ln}\left({x}\right) \\ $$$${case}\:\mathrm{2}\:{x}<\mathrm{0}\:\:{we}\:{follow}\:{the}\:{same}\:{method}\:. \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 21/Jul/18

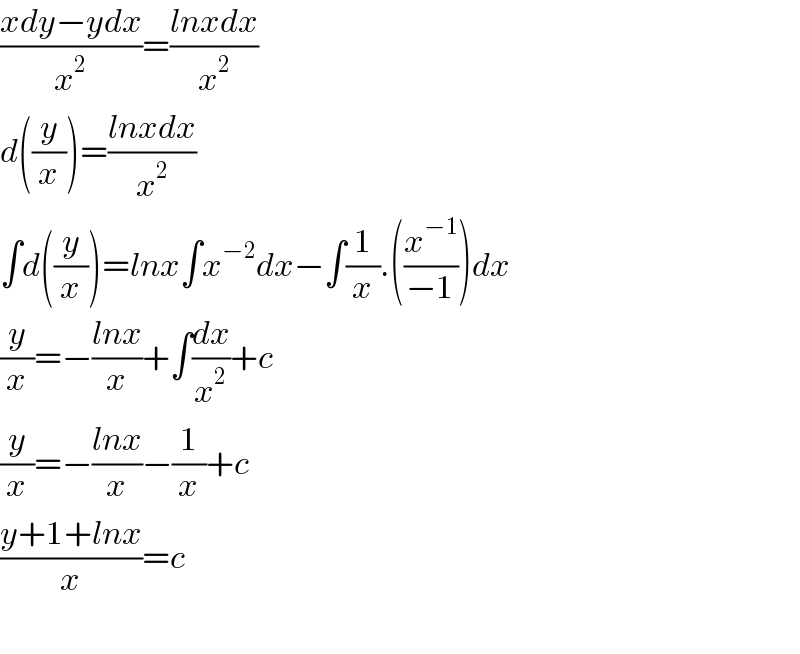
((xdy−ydx)/x^2 )=((lnxdx)/x^2 ) d((y/x))=((lnxdx)/x^2 ) ∫d((y/x))=lnx∫x^(−2) dx−∫(1/x).((x^(−1) /(−1)))dx (y/x)=−((lnx)/x)+∫(dx/x^2 )+c (y/x)=−((lnx)/x)−(1/x)+c ((y+1+lnx)/x)=c

$$\frac{{xdy}−{ydx}}{{x}^{\mathrm{2}} }=\frac{{lnxdx}}{{x}^{\mathrm{2}} } \\ $$$${d}\left(\frac{{y}}{{x}}\right)=\frac{{lnxdx}}{{x}^{\mathrm{2}} } \\ $$$$\int{d}\left(\frac{{y}}{{x}}\right)={lnx}\int{x}^{−\mathrm{2}} {dx}−\int\frac{\mathrm{1}}{{x}}.\left(\frac{{x}^{−\mathrm{1}} }{−\mathrm{1}}\right){dx} \\ $$$$\frac{{y}}{{x}}=−\frac{{lnx}}{{x}}+\int\frac{{dx}}{{x}^{\mathrm{2}} }+{c} \\ $$$$\frac{{y}}{{x}}=−\frac{{lnx}}{{x}}−\frac{\mathrm{1}}{{x}}+{c} \\ $$$$\frac{{y}+\mathrm{1}+{lnx}}{{x}}={c} \\ $$$$ \\ $$

Commented by rahul 19 last updated on 21/Jul/18

thank you sir ��

Terms of Service

Privacy Policy

Contact: info@tinkutara.com