
Previous in Differential Equation Next in Differential Equation
Question Number 14478 by tawa tawa last updated on 01/Jun/17
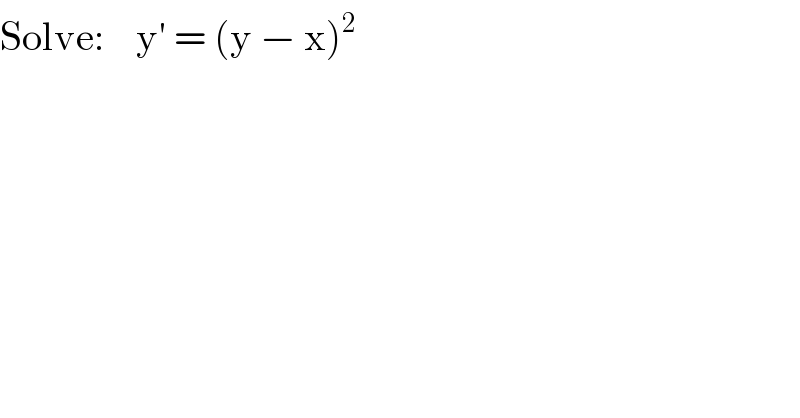
$$\mathrm{Solve}:\:\:\:\:\mathrm{y}'\:=\:\left(\mathrm{y}\:−\:\mathrm{x}\right)^{\mathrm{2}} \\ $$
Answered by mrW1 last updated on 01/Jun/17
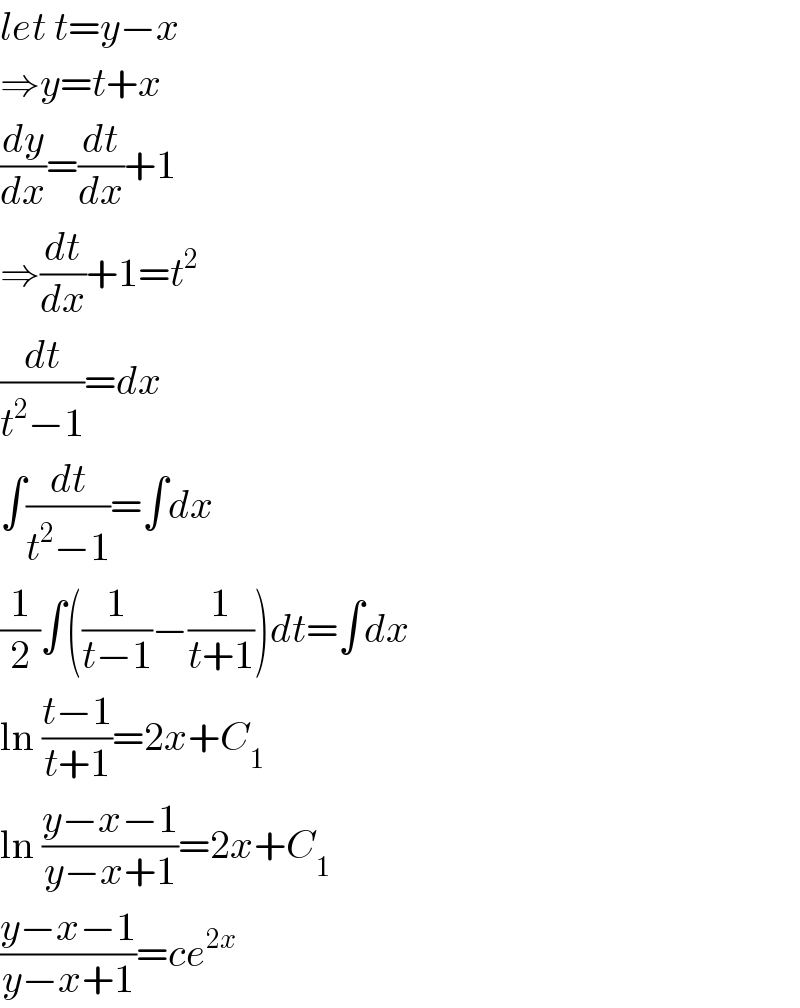
$${let}\:{t}={y}−{x} \\ $$$$\Rightarrow{y}={t}+{x} \\ $$$$\frac{{dy}}{{dx}}=\frac{{dt}}{{dx}}+\mathrm{1} \\ $$$$\Rightarrow\frac{{dt}}{{dx}}+\mathrm{1}={t}^{\mathrm{2}} \\ $$$$\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{1}}={dx} \\ $$$$\int\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{1}}=\int{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\left(\frac{\mathrm{1}}{{t}−\mathrm{1}}−\frac{\mathrm{1}}{{t}+\mathrm{1}}\right){dt}=\int{dx} \\ $$$$\mathrm{ln}\:\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}=\mathrm{2}{x}+{C}_{\mathrm{1}} \\ $$$$\mathrm{ln}\:\frac{{y}−{x}−\mathrm{1}}{{y}−{x}+\mathrm{1}}=\mathrm{2}{x}+{C}_{\mathrm{1}} \\ $$$$\frac{{y}−{x}−\mathrm{1}}{{y}−{x}+\mathrm{1}}={ce}^{\mathrm{2}{x}} \\ $$
Commented by tawa tawa last updated on 01/Jun/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 01/Jun/17
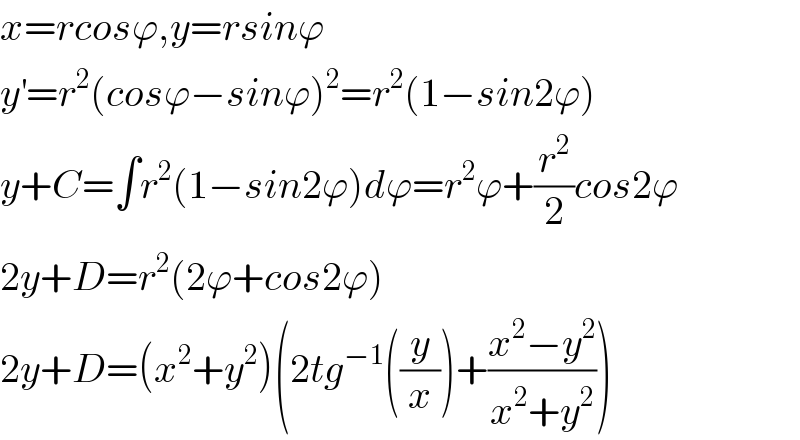
$${x}={rcos}\varphi,{y}={rsin}\varphi \\ $$$${y}^{'} ={r}^{\mathrm{2}} \left({cos}\varphi−{sin}\varphi\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \left(\mathrm{1}−{sin}\mathrm{2}\varphi\right) \\ $$$${y}+{C}=\int{r}^{\mathrm{2}} \left(\mathrm{1}−{sin}\mathrm{2}\varphi\right){d}\varphi={r}^{\mathrm{2}} \varphi+\frac{{r}^{\mathrm{2}} }{\mathrm{2}}{cos}\mathrm{2}\varphi \\ $$$$\mathrm{2}{y}+{D}={r}^{\mathrm{2}} \left(\mathrm{2}\varphi+{cos}\mathrm{2}\varphi\right) \\ $$$$\mathrm{2}{y}+{D}=\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\left(\mathrm{2}{tg}^{−\mathrm{1}} \left(\frac{{y}}{{x}}\right)+\frac{{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\right) \\ $$
Commented by tawa tawa last updated on 01/Jun/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
