
Question Number 201582 by deleted41 last updated on 09/Dec/23
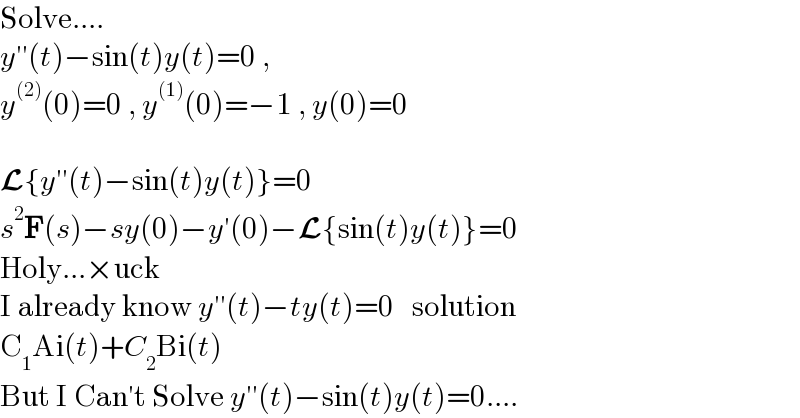
$$\mathrm{Solve}.... \\ $$$${y}''\left({t}\right)−\mathrm{sin}\left({t}\right){y}\left({t}\right)=\mathrm{0}\:,\: \\ $$$${y}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)=\mathrm{0}\:,\:{y}^{\left(\mathrm{1}\right)} \left(\mathrm{0}\right)=−\mathrm{1}\:,\:{y}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\boldsymbol{\mathcal{L}}\left\{{y}''\left({t}\right)−\mathrm{sin}\left({t}\right){y}\left({t}\right)\right\}=\mathrm{0} \\ $$$${s}^{\mathrm{2}} \boldsymbol{\mathrm{F}}\left({s}\right)−{sy}\left(\mathrm{0}\right)−{y}'\left(\mathrm{0}\right)−\boldsymbol{\mathcal{L}}\left\{\mathrm{sin}\left({t}\right){y}\left({t}\right)\right\}=\mathrm{0} \\ $$$$\mathrm{Holy}...×\mathrm{uck} \\ $$$$\mathrm{I}\:\mathrm{already}\:\mathrm{know}\:{y}''\left({t}\right)−{ty}\left({t}\right)=\mathrm{0}\:\:\:\mathrm{solution} \\ $$$$\mathrm{C}_{\mathrm{1}} \mathrm{Ai}\left({t}\right)+{C}_{\mathrm{2}} \mathrm{Bi}\left({t}\right) \\ $$$$\mathrm{But}\:\mathrm{I}\:\mathrm{Can}'\mathrm{t}\:\mathrm{Solve}\:{y}''\left({t}\right)−\mathrm{sin}\left({t}\right){y}\left({t}\right)=\mathrm{0}....\: \\ $$
