
Question Number 11268 by tawa last updated on 18/Mar/17

$$\mathrm{Solve}\:\mathrm{x},\:\mathrm{y}\:\mathrm{and}\:\mathrm{z}\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{p},\:\mathrm{q}\:\mathrm{and}\:\mathrm{r} \\ $$$$\mathrm{yz}\:=\:\mathrm{py}\:+\:\mathrm{qz}\:\:\:\:\:........\:\left(\mathrm{i}\right) \\ $$$$\mathrm{zx}\:=\:\mathrm{qz}\:+\:\mathrm{rx}\:\:\:\:\:\:.......\:\left(\mathrm{ii}\right) \\ $$$$\mathrm{xy}\:=\:\mathrm{rx}\:+\:\mathrm{py}\:\:\:\:\:.......\:\left(\mathrm{iii}\right) \\ $$
Answered by mrW1 last updated on 18/Mar/17
![(iii)⇒y=((rx)/(x−p)) (i)⇒z=((py)/(y−q))=(p/(1−(q/y)))=(p/(1−((q(x−p))/(rx)))) (ii)⇒z=((rx)/(x−q)) ⇒((rx)/(x−q))=(p/(1−((q(x−p))/(rx)))) rx[1−((q(x−p))/(rx))]=p(x−q) rx−q(x−p)=p(x−q) (p+q−r)x=2pq ⇒x=((2pq)/(p+q−r)) similarly ⇒y=((2qr)/(q+r−p)) ⇒z=((2pr)/(p+r−q))](Q11269.png)
$$\left({iii}\right)\Rightarrow{y}=\frac{{rx}}{{x}−{p}} \\ $$$$\left({i}\right)\Rightarrow{z}=\frac{{py}}{{y}−{q}}=\frac{{p}}{\mathrm{1}−\frac{{q}}{{y}}}=\frac{{p}}{\mathrm{1}−\frac{{q}\left({x}−{p}\right)}{{rx}}} \\ $$$$\left({ii}\right)\Rightarrow{z}=\frac{{rx}}{{x}−{q}} \\ $$$$\Rightarrow\frac{{rx}}{{x}−{q}}=\frac{{p}}{\mathrm{1}−\frac{{q}\left({x}−{p}\right)}{{rx}}} \\ $$$${rx}\left[\mathrm{1}−\frac{{q}\left({x}−{p}\right)}{{rx}}\right]={p}\left({x}−{q}\right) \\ $$$${rx}−{q}\left({x}−{p}\right)={p}\left({x}−{q}\right) \\ $$$$\left({p}+{q}−{r}\right){x}=\mathrm{2}{pq} \\ $$$$\Rightarrow{x}=\frac{\mathrm{2}{pq}}{{p}+{q}−{r}} \\ $$$${similarly} \\ $$$$\Rightarrow{y}=\frac{\mathrm{2}{qr}}{{q}+{r}−{p}} \\ $$$$\Rightarrow{z}=\frac{\mathrm{2}{pr}}{{p}+{r}−{q}} \\ $$
Commented by tawa last updated on 18/Mar/17
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}. \\ $$
Commented by tawa last updated on 18/Mar/17

$$\mathrm{please}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{need}\:\mathrm{the}\:\mathrm{cubic}\:\mathrm{equation}\:\mathrm{formulars}\:\mathrm{you}\:\mathrm{posted}\:\mathrm{sometimes}\:\mathrm{ago}. \\ $$
Commented by mrW1 last updated on 18/Mar/17

Commented by tawa last updated on 18/Mar/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 19/Mar/17
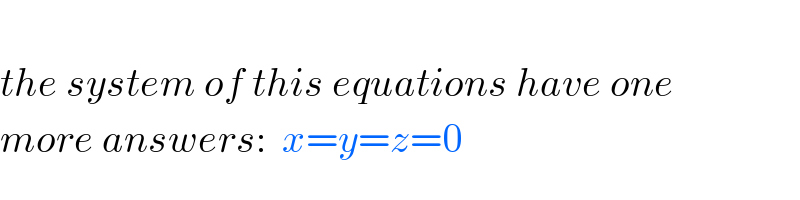
$$ \\ $$$${the}\:{system}\:{of}\:{this}\:{equations}\:{have}\:{one} \\ $$$${more}\:{answers}:\:\:{x}={y}={z}=\mathrm{0} \\ $$
Commented by mrW1 last updated on 19/Mar/17
$${you}\:{are}\:{right}.\:{this}\:{case}\:{should}\:{be}\:{considered} \\ $$$${in}\:{the}\:{step}\:\mathrm{2}. \\ $$
