
Question Number 15501 by rish@bh last updated on 11/Jun/17

$$\mathrm{Solve} \\ $$$${x}^{\mathrm{3}} −\lfloor{x}\rfloor=\mathrm{3} \\ $$
Answered by mrW1 last updated on 11/Jun/17
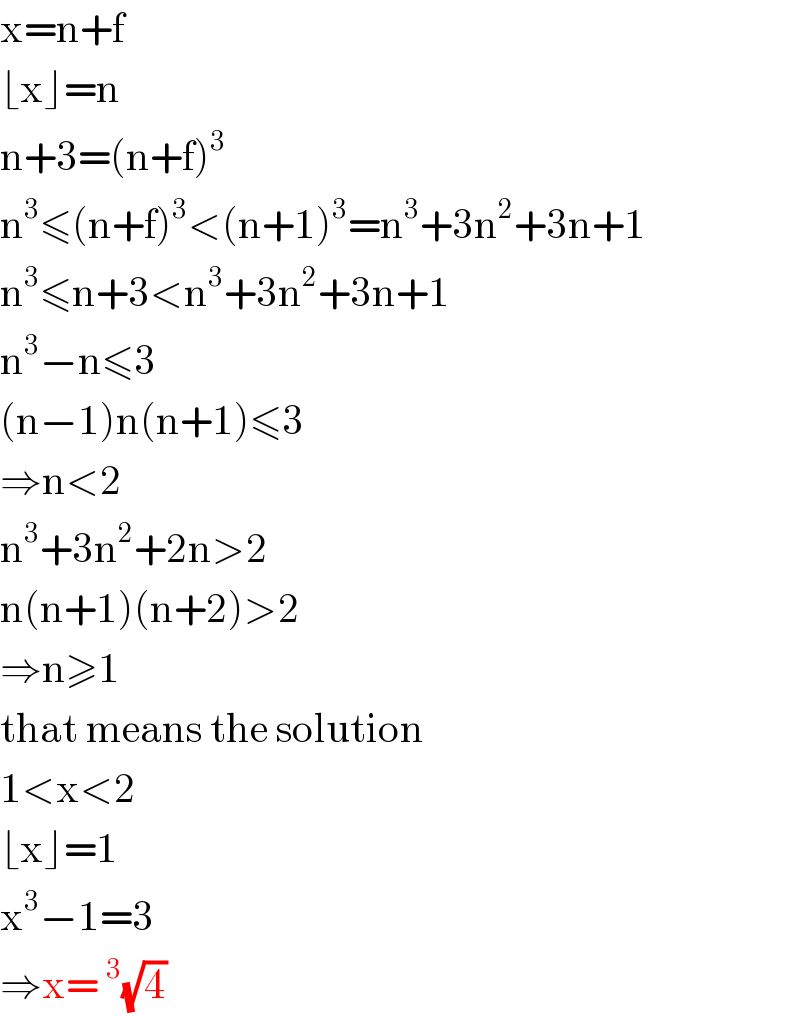
$$\mathrm{x}=\mathrm{n}+\mathrm{f} \\ $$$$\lfloor\mathrm{x}\rfloor=\mathrm{n} \\ $$$$\mathrm{n}+\mathrm{3}=\left(\mathrm{n}+\mathrm{f}\right)^{\mathrm{3}} \\ $$$$\mathrm{n}^{\mathrm{3}} \leqslant\left(\mathrm{n}+\mathrm{f}\right)^{\mathrm{3}} <\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{3}} =\mathrm{n}^{\mathrm{3}} +\mathrm{3n}^{\mathrm{2}} +\mathrm{3n}+\mathrm{1} \\ $$$$\mathrm{n}^{\mathrm{3}} \leqslant\mathrm{n}+\mathrm{3}<\mathrm{n}^{\mathrm{3}} +\mathrm{3n}^{\mathrm{2}} +\mathrm{3n}+\mathrm{1} \\ $$$$\mathrm{n}^{\mathrm{3}} −\mathrm{n}\leqslant\mathrm{3} \\ $$$$\left(\mathrm{n}−\mathrm{1}\right)\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\leqslant\mathrm{3} \\ $$$$\Rightarrow\mathrm{n}<\mathrm{2} \\ $$$$\mathrm{n}^{\mathrm{3}} +\mathrm{3n}^{\mathrm{2}} +\mathrm{2n}>\mathrm{2} \\ $$$$\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{2}\right)>\mathrm{2} \\ $$$$\Rightarrow\mathrm{n}\geqslant\mathrm{1} \\ $$$$\mathrm{that}\:\mathrm{means}\:\mathrm{the}\:\mathrm{solution} \\ $$$$\mathrm{1}<\mathrm{x}<\mathrm{2} \\ $$$$\lfloor\mathrm{x}\rfloor=\mathrm{1} \\ $$$$\mathrm{x}^{\mathrm{3}} −\mathrm{1}=\mathrm{3} \\ $$$$\Rightarrow\mathrm{x}=\:^{\mathrm{3}} \sqrt{\mathrm{4}} \\ $$
