
Previous in Differential Equation Next in Differential Equation
Question Number 43616 by Tawa1 last updated on 12/Sep/18
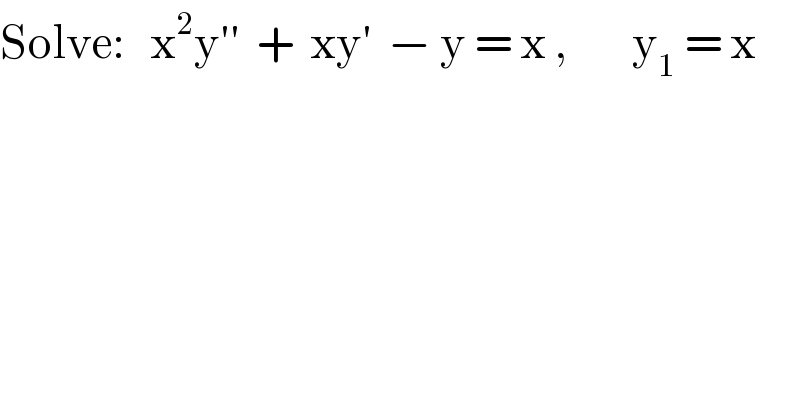
$$\mathrm{Solve}:\:\:\:\mathrm{x}^{\mathrm{2}} \mathrm{y}''\:\:+\:\:\mathrm{xy}'\:\:−\:\mathrm{y}\:=\:\mathrm{x}\:,\:\:\:\:\:\:\:\:\mathrm{y}_{\mathrm{1}} \:=\:\mathrm{x} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 13/Sep/18
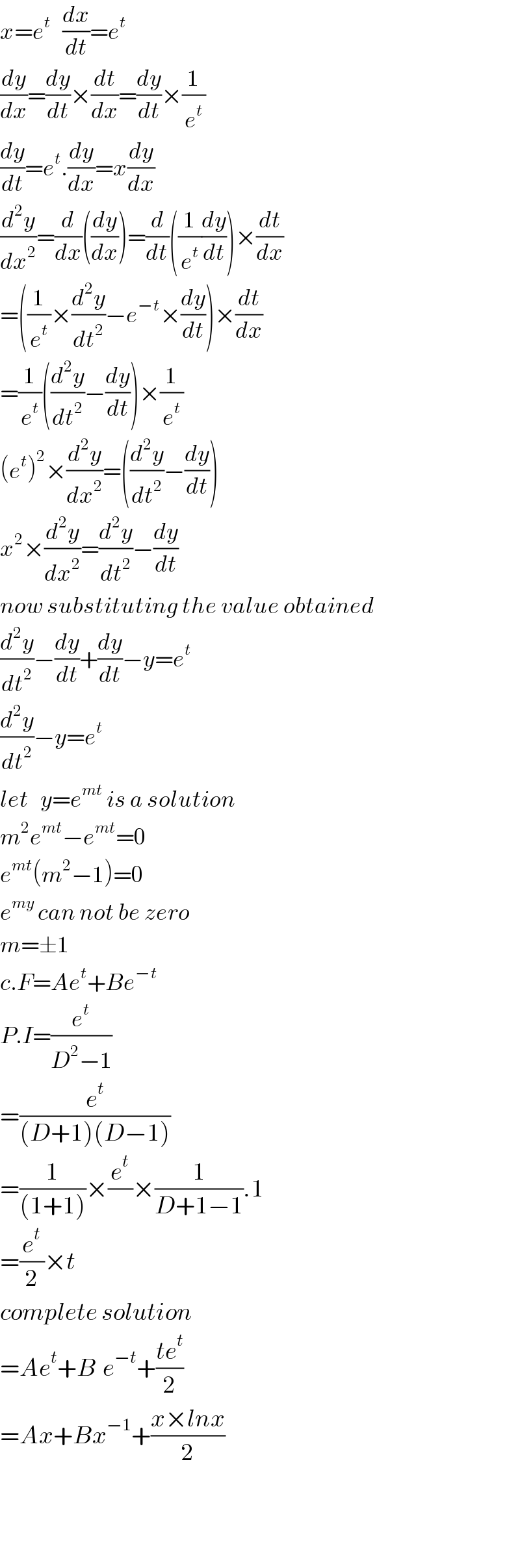
$${x}={e}^{{t}} \:\:\:\frac{{dx}}{{dt}}={e}^{{t}} \\ $$$$\frac{{dy}}{{dx}}=\frac{{dy}}{{dt}}×\frac{{dt}}{{dx}}=\frac{{dy}}{{dt}}×\frac{\mathrm{1}}{{e}^{{t}} } \\ $$$$\frac{{dy}}{{dt}}={e}^{{t}} .\frac{{dy}}{{dx}}={x}\frac{{dy}}{{dx}} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{{d}}{{dx}}\left(\frac{{dy}}{{dx}}\right)=\frac{{d}}{{dt}}\left(\frac{\mathrm{1}}{{e}^{{t}} }\frac{{dy}}{{dt}}\right)×\frac{{dt}}{{dx}} \\ $$$$=\left(\frac{\mathrm{1}}{{e}^{{t}} }×\frac{{d}^{\mathrm{2}} {y}}{{dt}^{\mathrm{2}} }−{e}^{−{t}} ×\frac{{dy}}{{dt}}\right)×\frac{{dt}}{{dx}} \\ $$$$=\frac{\mathrm{1}}{{e}^{{t}} }\left(\frac{{d}^{\mathrm{2}} {y}}{{dt}^{\mathrm{2}} }−\frac{{dy}}{{dt}}\right)×\frac{\mathrm{1}}{{e}^{{t}} } \\ $$$$\left({e}^{{t}} \right)^{\mathrm{2}} ×\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\left(\frac{{d}^{\mathrm{2}} {y}}{{dt}^{\mathrm{2}} }−\frac{{dy}}{{dt}}\right) \\ $$$${x}^{\mathrm{2}} ×\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{{d}^{\mathrm{2}} {y}}{{dt}^{\mathrm{2}} }−\frac{{dy}}{{dt}} \\ $$$${now}\:{substituting}\:{the}\:{value}\:{obtained} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dt}^{\mathrm{2}} }−\frac{{dy}}{{dt}}+\frac{{dy}}{{dt}}−{y}={e}^{{t}} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dt}^{\mathrm{2}} }−{y}={e}^{{t}} \\ $$$${let}\:\:\:{y}={e}^{{mt}} \:{is}\:{a}\:{solution} \\ $$$${m}^{\mathrm{2}} {e}^{{mt}} −{e}^{{mt}} =\mathrm{0} \\ $$$${e}^{{mt}} \left({m}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{0} \\ $$$${e}^{{my}} \:{can}\:{not}\:{be}\:{zero} \\ $$$${m}=\pm\mathrm{1} \\ $$$${c}.{F}={Ae}^{{t}} +{Be}^{−{t}} \\ $$$${P}.{I}=\frac{{e}^{{t}} }{{D}^{\mathrm{2}} −\mathrm{1}} \\ $$$$=\frac{{e}^{{t}} }{\left({D}+\mathrm{1}\right)\left({D}−\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{1}\right)}×\frac{{e}^{{t}} }{}×\frac{\mathrm{1}}{{D}+\mathrm{1}−\mathrm{1}}.\mathrm{1} \\ $$$$=\frac{{e}^{{t}} }{\mathrm{2}}×{t} \\ $$$${complete}\:{solution} \\ $$$$={Ae}^{{t}} +{B}^{} {e}^{−{t}} +\frac{{te}^{{t}} }{\mathrm{2}} \\ $$$$={Ax}+{Bx}^{−\mathrm{1}} +\frac{{x}×{lnx}}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$
Commented by Tawa1 last updated on 13/Sep/18
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
