
Question Number 215356 by Abdullahrussell last updated on 04/Jan/25
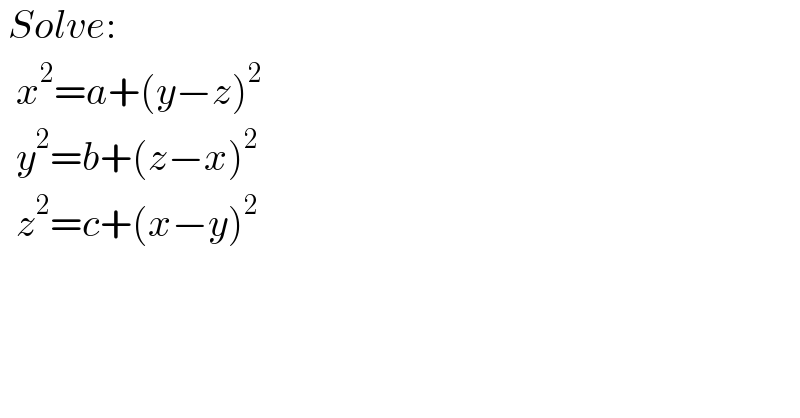
$$\:{Solve}: \\ $$$$\:\:{x}^{\mathrm{2}} ={a}+\left({y}−{z}\right)^{\mathrm{2}} \\ $$$$\:\:{y}^{\mathrm{2}} ={b}+\left({z}−{x}\right)^{\mathrm{2}} \\ $$$$\:\:{z}^{\mathrm{2}} ={c}+\left({x}−{y}\right)^{\mathrm{2}} \\ $$
Answered by mr W last updated on 04/Jan/25
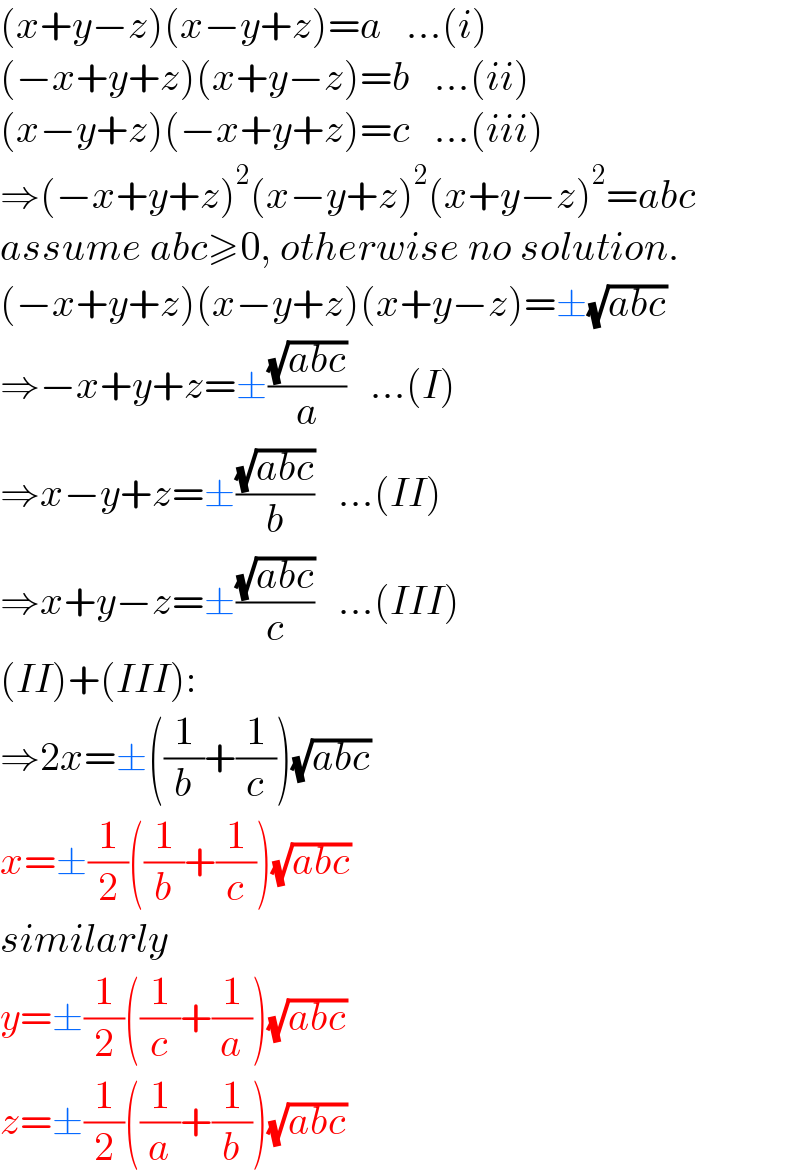
$$\left({x}+{y}−{z}\right)\left({x}−{y}+{z}\right)={a}\:\:\:...\left({i}\right) \\ $$$$\left(−{x}+{y}+{z}\right)\left({x}+{y}−{z}\right)={b}\:\:\:...\left({ii}\right) \\ $$$$\left({x}−{y}+{z}\right)\left(−{x}+{y}+{z}\right)={c}\:\:\:...\left({iii}\right) \\ $$$$\Rightarrow\left(−{x}+{y}+{z}\right)^{\mathrm{2}} \left({x}−{y}+{z}\right)^{\mathrm{2}} \left({x}+{y}−{z}\right)^{\mathrm{2}} ={abc} \\ $$$${assume}\:{abc}\geqslant\mathrm{0},\:{otherwise}\:{no}\:{solution}. \\ $$$$\left(−{x}+{y}+{z}\right)\left({x}−{y}+{z}\right)\left({x}+{y}−{z}\right)=\pm\sqrt{{abc}} \\ $$$$\Rightarrow−{x}+{y}+{z}=\pm\frac{\sqrt{{abc}}}{{a}}\:\:\:...\left({I}\right) \\ $$$$\Rightarrow{x}−{y}+{z}=\pm\frac{\sqrt{{abc}}}{{b}}\:\:\:...\left({II}\right) \\ $$$$\Rightarrow{x}+{y}−{z}=\pm\frac{\sqrt{{abc}}}{{c}}\:\:\:...\left({III}\right) \\ $$$$\left({II}\right)+\left({III}\right): \\ $$$$\Rightarrow\mathrm{2}{x}=\pm\left(\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}\right)\sqrt{{abc}} \\ $$$${x}=\pm\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}\right)\sqrt{{abc}} \\ $$$${similarly} \\ $$$${y}=\pm\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{{c}}+\frac{\mathrm{1}}{{a}}\right)\sqrt{{abc}} \\ $$$${z}=\pm\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}\right)\sqrt{{abc}} \\ $$
