
Question Number 114592 by Aziztisffola last updated on 19/Sep/20
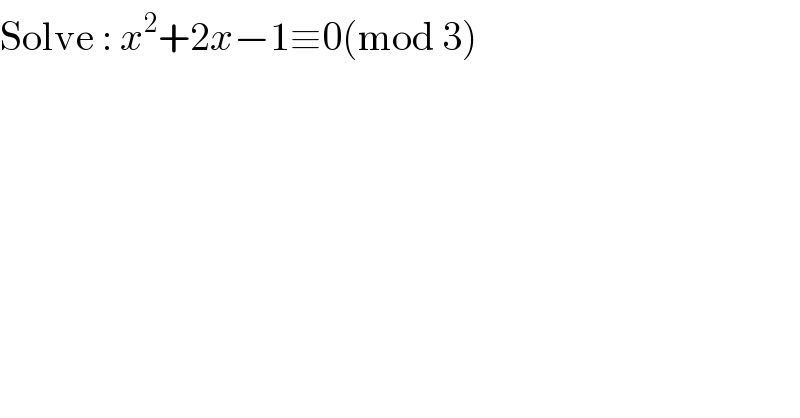
$$\mathrm{Solve}\::\:{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{1}\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{3}\right) \\ $$
Answered by MJS_new last updated on 19/Sep/20
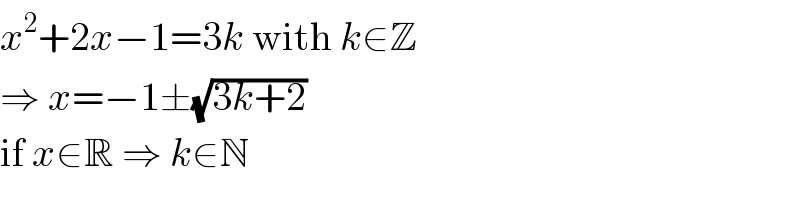
$${x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{1}=\mathrm{3}{k}\:\mathrm{with}\:{k}\in\mathbb{Z} \\ $$$$\Rightarrow\:{x}=−\mathrm{1}\pm\sqrt{\mathrm{3}{k}+\mathrm{2}} \\ $$$$\mathrm{if}\:{x}\in\mathbb{R}\:\Rightarrow\:{k}\in\mathbb{N} \\ $$
Commented by Aziztisffola last updated on 19/Sep/20
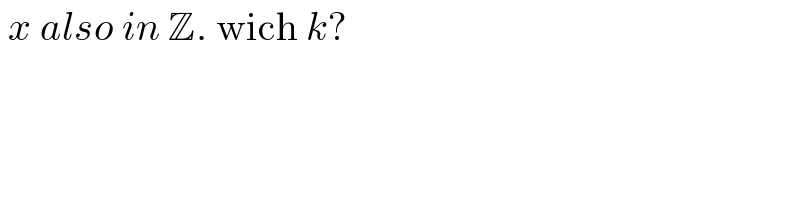
$$\:{x}\:{also}\:{in}\:\mathbb{Z}.\:\mathrm{wich}\:{k}? \\ $$
Commented by Aziztisffola last updated on 19/Sep/20
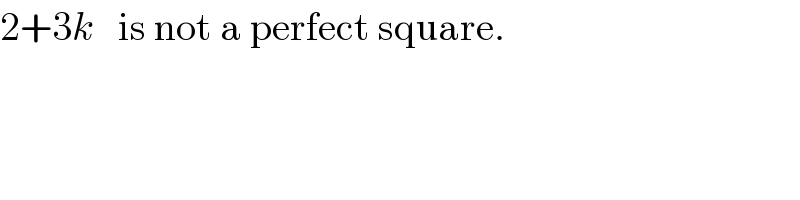
$$\mathrm{2}+\mathrm{3}{k}\:\:\:\mathrm{is}\:\mathrm{not}\:\mathrm{a}\:\mathrm{perfect}\:\mathrm{square}. \\ $$
Commented by MJS_new last updated on 19/Sep/20

$$\mathrm{there}'\mathrm{s}\:\mathrm{no}\:{x}\in\mathbb{Z} \\ $$
Commented by Aziztisffola last updated on 19/Sep/20
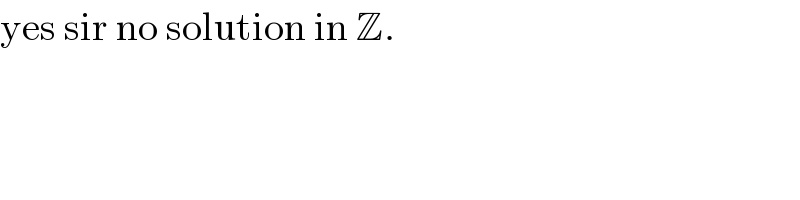
$$\mathrm{yes}\:\mathrm{sir}\:\mathrm{no}\:\mathrm{solution}\:\mathrm{in}\:\mathbb{Z}. \\ $$
Answered by floor(10²Eta[1]) last updated on 19/Sep/20
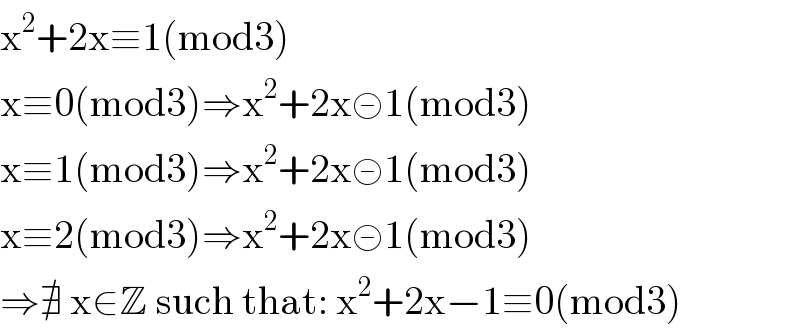
$$\mathrm{x}^{\mathrm{2}} +\mathrm{2x}\equiv\mathrm{1}\left(\mathrm{mod3}\right) \\ $$$$\mathrm{x}\equiv\mathrm{0}\left(\mathrm{mod3}\right)\Rightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{2x}≢\mathrm{1}\left(\mathrm{mod3}\right) \\ $$$$\mathrm{x}\equiv\mathrm{1}\left(\mathrm{mod3}\right)\Rightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{2x}≢\mathrm{1}\left(\mathrm{mod3}\right) \\ $$$$\mathrm{x}\equiv\mathrm{2}\left(\mathrm{mod3}\right)\Rightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{2x}≢\mathrm{1}\left(\mathrm{mod3}\right) \\ $$$$\Rightarrow\nexists\:\mathrm{x}\in\mathbb{Z}\:\mathrm{such}\:\mathrm{that}:\:\mathrm{x}^{\mathrm{2}} +\mathrm{2x}−\mathrm{1}\equiv\mathrm{0}\left(\mathrm{mod3}\right) \\ $$
Commented by Aziztisffola last updated on 19/Sep/20
![yes sir that′s it. x^2 +2x−1≡0(mod3) ⇔(x+1)^2 ≡2[3] ⇔(x+1)^2 =2+3k /k∈Z and 2+3k≠ n^2 for n in Z. then no solution.](Q114610.png)
$$\mathrm{yes}\:\mathrm{sir}\:\mathrm{that}'\mathrm{s}\:\mathrm{it}. \\ $$$$\:\mathrm{x}^{\mathrm{2}} +\mathrm{2x}−\mathrm{1}\equiv\mathrm{0}\left(\mathrm{mod3}\right) \\ $$$$\Leftrightarrow\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \equiv\mathrm{2}\left[\mathrm{3}\right] \\ $$$$\Leftrightarrow\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{2}+\mathrm{3k}\:\:/\mathrm{k}\in\mathbb{Z} \\ $$$$\:\mathrm{and}\:\mathrm{2}+\mathrm{3k}\neq\:\mathrm{n}^{\mathrm{2}} \:\:\mathrm{for}\:\mathrm{n}\:\mathrm{in}\:\mathbb{Z}. \\ $$$$\mathrm{then}\:\mathrm{no}\:\mathrm{solution}. \\ $$
Answered by 1549442205PVT last updated on 20/Sep/20

$$\:{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{1}\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{3}\right)\left(\ast\right) \\ $$$$\forall\mathrm{x}\in\mathbb{Z}\:\mathrm{we}\:\mathrm{always}\:\mathrm{have}\:\mathrm{x}=\mathrm{3k}\pm\mathrm{1or}\:\mathrm{x}=\mathrm{3k} \\ $$$$\left.\mathrm{i}\right)\mathrm{If}\:\mathrm{x}=\mathrm{3k}\:\mathrm{then}\:\mathrm{x}^{\mathrm{2}} +\mathrm{2x}−\mathrm{1}=−\mathrm{1}\left(\mathrm{mod3}\right) \\ $$$$\Rightarrow\left(\ast\right)\mathrm{has}\:\mathrm{no}\:\mathrm{roots}\left(\mathrm{1}\right) \\ $$$$\left.\mathrm{ii}\right)\mathrm{If}\:\mathrm{x}=\mathrm{3k}+\mathrm{1}\:\mathrm{then}\:\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}= \\ $$$$\left.\left(\mathrm{3k}+\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2}=\mathrm{9k}^{\mathrm{2}} +\mathrm{12k}+\mathrm{2}\right)=\mathrm{2}\left(\mathrm{mod3}\right)\left(\mathrm{2}\right) \\ $$$$\left.\mathrm{iii}\right)\mathrm{If}\:\mathrm{x}=\mathrm{3k}−\mathrm{1}\:\mathrm{then}\:\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}=\mathrm{9k}^{\mathrm{2}} −\mathrm{2} \\ $$$$=−\mathrm{2}\left(\mathrm{mod3}\right)\left(\mathrm{3}\right) \\ $$$$\mathrm{From}\:\left(\mathrm{1}\right)\left(\mathrm{2}\right)\left(\mathrm{3}\right)\:\mathrm{infer}\:\mathrm{the}\:\mathrm{equation}\left(\ast\right) \\ $$$$\mathrm{has}\:\mathrm{no}\:\mathrm{roots}\:\mathrm{in}\:\mathbb{Z} \\ $$
