
Question Number 171664 by LEKOUMA last updated on 19/Jun/22
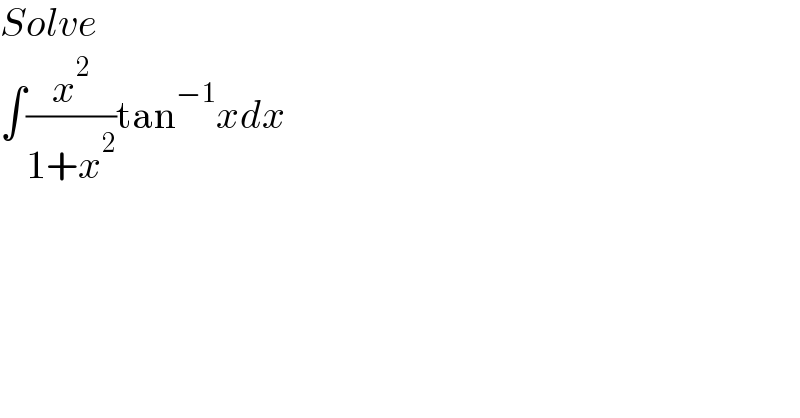
$${Solve} \\ $$$$\int\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }\mathrm{tan}^{−\mathrm{1}} {xdx} \\ $$
Commented by infinityaction last updated on 19/Jun/22
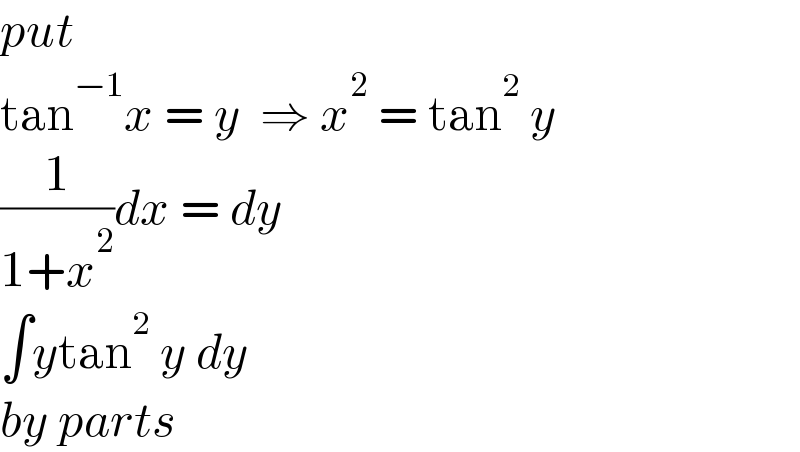
$${put}\: \\ $$$$\mathrm{tan}^{−\mathrm{1}} {x}\:=\:{y}\:\:\Rightarrow\:{x}^{\mathrm{2}} \:=\:\mathrm{tan}^{\mathrm{2}} \:{y} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:=\:{dy} \\ $$$$\int{y}\mathrm{tan}^{\mathrm{2}} \:{y}\:{dy} \\ $$$${by}\:{parts} \\ $$
Answered by mindispower last updated on 19/Jun/22
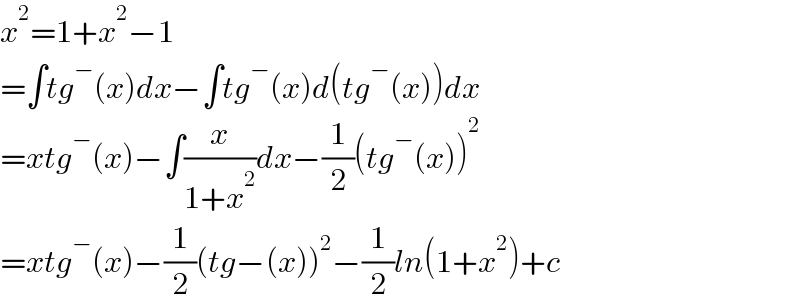
$${x}^{\mathrm{2}} =\mathrm{1}+{x}^{\mathrm{2}} −\mathrm{1} \\ $$$$=\int{tg}^{−} \left({x}\right){dx}−\int{tg}^{−} \left({x}\right){d}\left({tg}^{−} \left({x}\right)\right){dx} \\ $$$$={xtg}^{−} \left({x}\right)−\int\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}−\frac{\mathrm{1}}{\mathrm{2}}\left({tg}^{−} \left({x}\right)\right)^{\mathrm{2}} \\ $$$$={xtg}^{−} \left({x}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left({tg}−\left({x}\right)\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)+{c} \\ $$
