
Previous in Relation and Functions Next in Relation and Functions
Question Number 17872 by Tinkutara last updated on 11/Jul/17
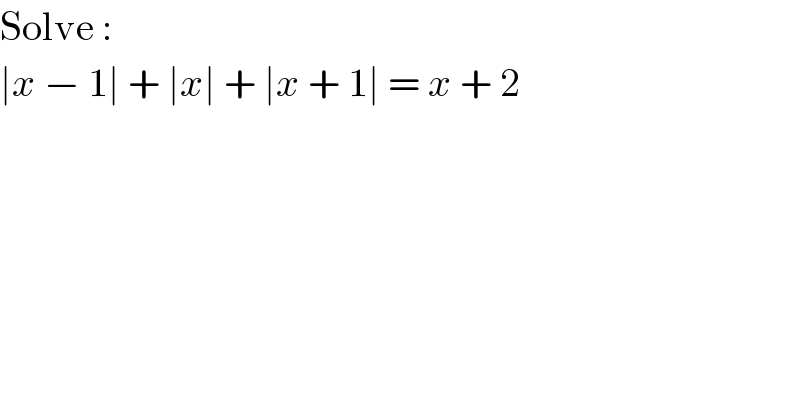
$$\mathrm{Solve}\:: \\ $$$$\mid{x}\:−\:\mathrm{1}\mid\:+\:\mid{x}\mid\:+\:\mid{x}\:+\:\mathrm{1}\mid\:=\:{x}\:+\:\mathrm{2} \\ $$
Answered by ajfour last updated on 11/Jul/17
![x∈[0, 1]](Q17875.png)
$$\:\:\:\mathrm{x}\in\left[\mathrm{0},\:\mathrm{1}\right] \\ $$
Answered by ajfour last updated on 12/Jul/17
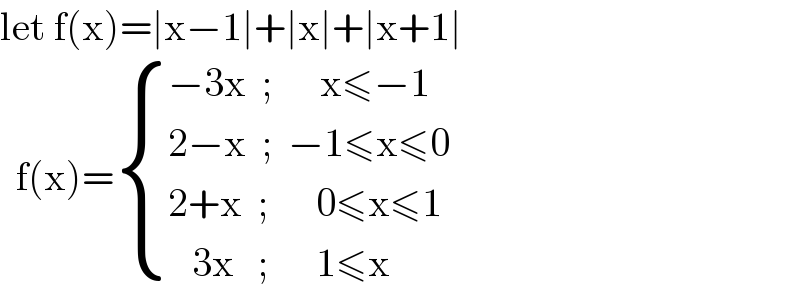
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\mid\mathrm{x}−\mathrm{1}\mid+\mid\mathrm{x}\mid+\mid\mathrm{x}+\mathrm{1}\mid \\ $$$$\:\:\mathrm{f}\left(\mathrm{x}\right)=\begin{cases}{−\mathrm{3x}\:\:;\:\:\:\:\:\:\mathrm{x}\leqslant−\mathrm{1}}\\{\mathrm{2}−\mathrm{x}\:\:;\:\:−\mathrm{1}\leqslant\mathrm{x}\leqslant\mathrm{0}}\\{\mathrm{2}+\mathrm{x}\:\:;\:\:\:\:\:\:\mathrm{0}\leqslant\mathrm{x}\leqslant\mathrm{1}}\\{\:\:\:\mathrm{3x}\:\:\:;\:\:\:\:\:\:\mathrm{1}\leqslant\mathrm{x}}\end{cases} \\ $$
Commented by ajfour last updated on 12/Jul/17
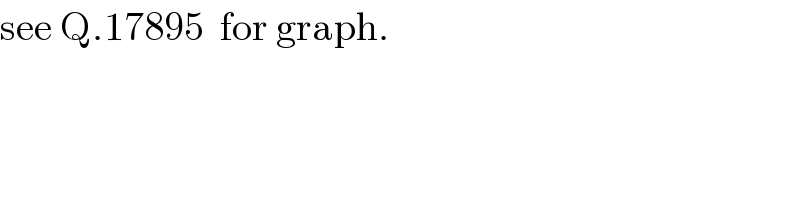
$$\mathrm{see}\:\mathrm{Q}.\mathrm{17895}\:\:\mathrm{for}\:\mathrm{graph}. \\ $$
Commented by Tinkutara last updated on 12/Jul/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
