
Question Number 18904 by Satyamtt last updated on 01/Aug/17
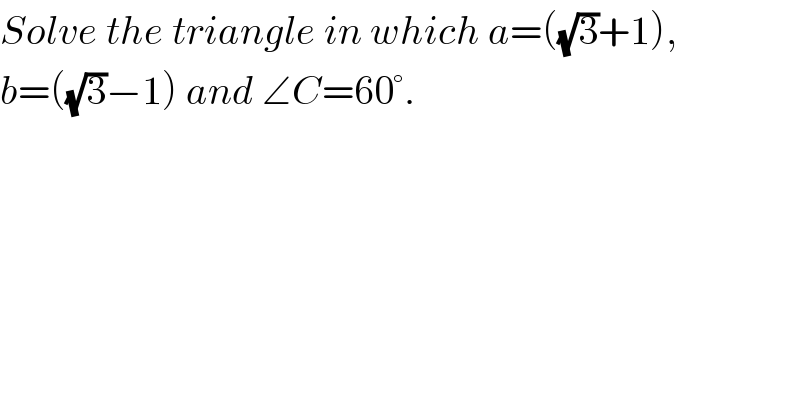
$${Solve}\:{the}\:{triangle}\:{in}\:{which}\:{a}=\left(\sqrt{\mathrm{3}}+\mathrm{1}\right),\: \\ $$$${b}=\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)\:{and}\:\angle{C}=\mathrm{60}°. \\ $$$$ \\ $$
Answered by behi.8.3.4.1.7@gmail.com last updated on 01/Aug/17
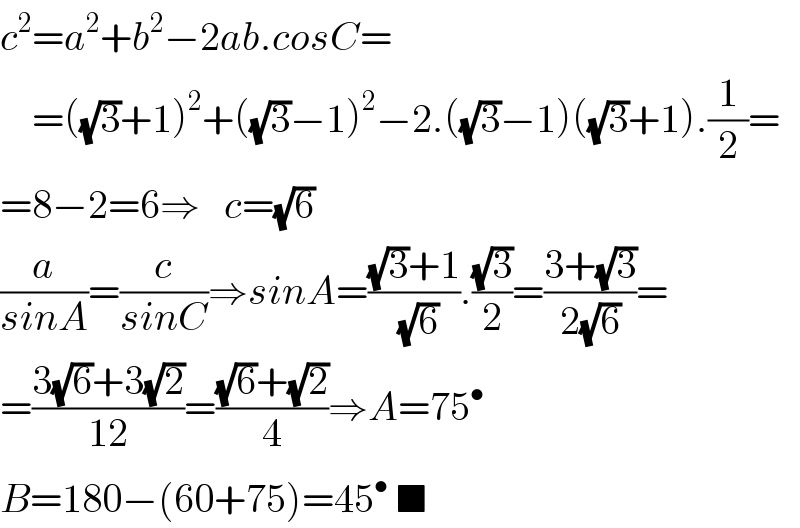
$${c}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}.{cosC}= \\ $$$$\:\:\:\:=\left(\sqrt{\mathrm{3}}+\mathrm{1}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}.\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)\left(\sqrt{\mathrm{3}}+\mathrm{1}\right).\frac{\mathrm{1}}{\mathrm{2}}= \\ $$$$=\mathrm{8}−\mathrm{2}=\mathrm{6}\Rightarrow\:\:\:{c}=\sqrt{\mathrm{6}} \\ $$$$\frac{{a}}{{sinA}}=\frac{{c}}{{sinC}}\Rightarrow{sinA}=\frac{\sqrt{\mathrm{3}}+\mathrm{1}}{\sqrt{\mathrm{6}}}.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=\frac{\mathrm{3}+\sqrt{\mathrm{3}}}{\mathrm{2}\sqrt{\mathrm{6}}}= \\ $$$$=\frac{\mathrm{3}\sqrt{\mathrm{6}}+\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{12}}=\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\mathrm{4}}\Rightarrow{A}=\mathrm{75}^{\bullet} \\ $$$${B}=\mathrm{180}−\left(\mathrm{60}+\mathrm{75}\right)=\mathrm{45}^{\bullet} \:\blacksquare \\ $$
