
Question Number 46785 by Tawa1 last updated on 31/Oct/18
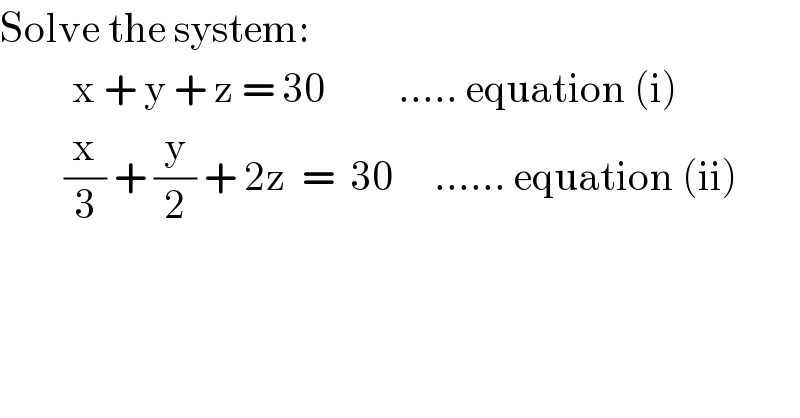
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{system}: \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{x}\:+\:\mathrm{y}\:+\:\mathrm{z}\:=\:\mathrm{30}\:\:\:\:\:\:\:\:\:.....\:\mathrm{equation}\:\left(\mathrm{i}\right) \\ $$$$\:\:\:\:\:\:\:\:\frac{\mathrm{x}}{\mathrm{3}}\:+\:\frac{\mathrm{y}}{\mathrm{2}}\:+\:\mathrm{2z}\:\:=\:\:\mathrm{30}\:\:\:\:\:......\:\mathrm{equation}\:\left(\mathrm{ii}\right) \\ $$$$\:\:\:\:\:\:\:\: \\ $$
Answered by MJS last updated on 31/Oct/18
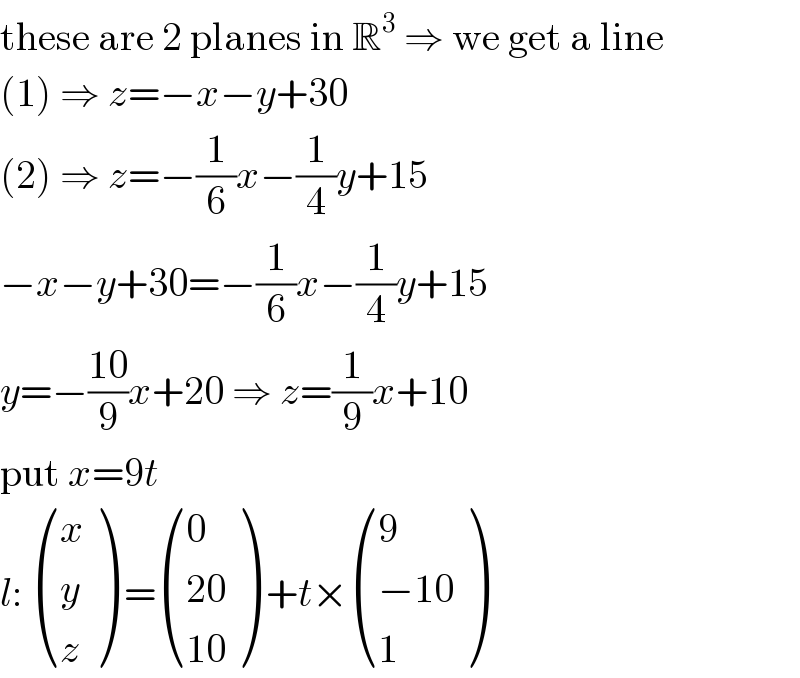
$$\mathrm{these}\:\mathrm{are}\:\mathrm{2}\:\mathrm{planes}\:\mathrm{in}\:\mathbb{R}^{\mathrm{3}} \:\Rightarrow\:\mathrm{we}\:\mathrm{get}\:\mathrm{a}\:\mathrm{line} \\ $$$$\left(\mathrm{1}\right)\:\Rightarrow\:{z}=−{x}−{y}+\mathrm{30} \\ $$$$\left(\mathrm{2}\right)\:\Rightarrow\:{z}=−\frac{\mathrm{1}}{\mathrm{6}}{x}−\frac{\mathrm{1}}{\mathrm{4}}{y}+\mathrm{15} \\ $$$$−{x}−{y}+\mathrm{30}=−\frac{\mathrm{1}}{\mathrm{6}}{x}−\frac{\mathrm{1}}{\mathrm{4}}{y}+\mathrm{15} \\ $$$${y}=−\frac{\mathrm{10}}{\mathrm{9}}{x}+\mathrm{20}\:\Rightarrow\:{z}=\frac{\mathrm{1}}{\mathrm{9}}{x}+\mathrm{10} \\ $$$$\mathrm{put}\:{x}=\mathrm{9}{t} \\ $$$${l}:\:\begin{pmatrix}{{x}}\\{{y}}\\{{z}}\end{pmatrix}\:=\begin{pmatrix}{\mathrm{0}}\\{\mathrm{20}}\\{\mathrm{10}}\end{pmatrix}\:+{t}×\begin{pmatrix}{\mathrm{9}}\\{−\mathrm{10}}\\{\mathrm{1}}\end{pmatrix} \\ $$
Commented by Tawa1 last updated on 31/Oct/18
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
