Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 168053 by lapache last updated on 01/Apr/22

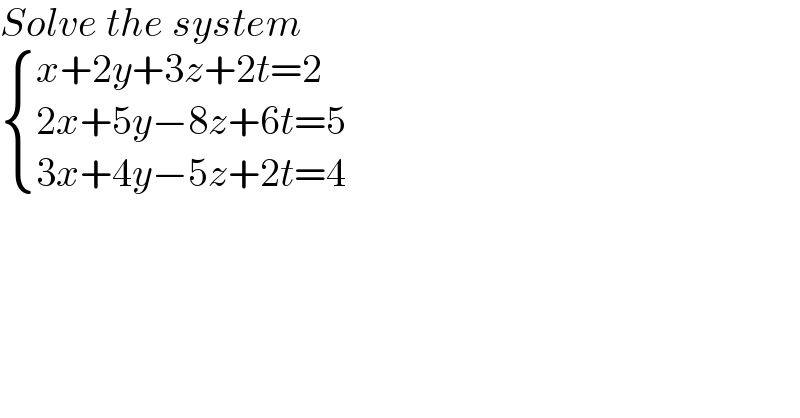
Solve the system { ((x+2y+3z+2t=2)),((2x+5y−8z+6t=5)),((3x+4y−5z+2t=4)) :}

$${Solve}\:{the}\:{system}\: \\ $$$$\begin{cases}{{x}+\mathrm{2}{y}+\mathrm{3}{z}+\mathrm{2}{t}=\mathrm{2}}\\{\mathrm{2}{x}+\mathrm{5}{y}−\mathrm{8}{z}+\mathrm{6}{t}=\mathrm{5}}\\{\mathrm{3}{x}+\mathrm{4}{y}−\mathrm{5}{z}+\mathrm{2}{t}=\mathrm{4}}\end{cases} \\ $$

Answered by MJS_new last updated on 01/Apr/22

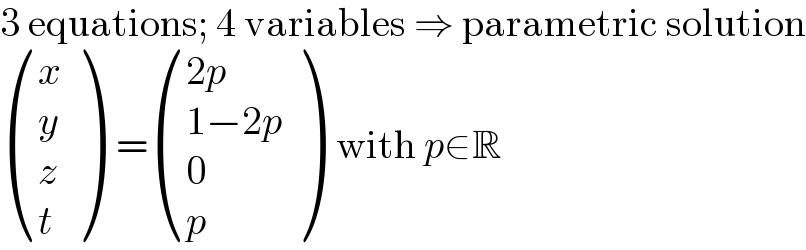
3 equations; 4 variables ⇒ parametric solution ((x),(y),(z),(t) ) = (((2p)),((1−2p)),(0),(p) ) with p∈R

$$\mathrm{3}\:\mathrm{equations};\:\mathrm{4}\:\mathrm{variables}\:\Rightarrow\:\mathrm{parametric}\:\mathrm{solution} \\ $$$$\begin{pmatrix}{{x}}\\{{y}}\\{{z}}\\{{t}}\end{pmatrix}\:\:=\begin{pmatrix}{\mathrm{2}{p}}\\{\mathrm{1}−\mathrm{2}{p}}\\{\mathrm{0}}\\{{p}}\end{pmatrix}\:\:\mathrm{with}\:{p}\in\mathbb{R} \\ $$

Answered by FelipeLz last updated on 03/Apr/22

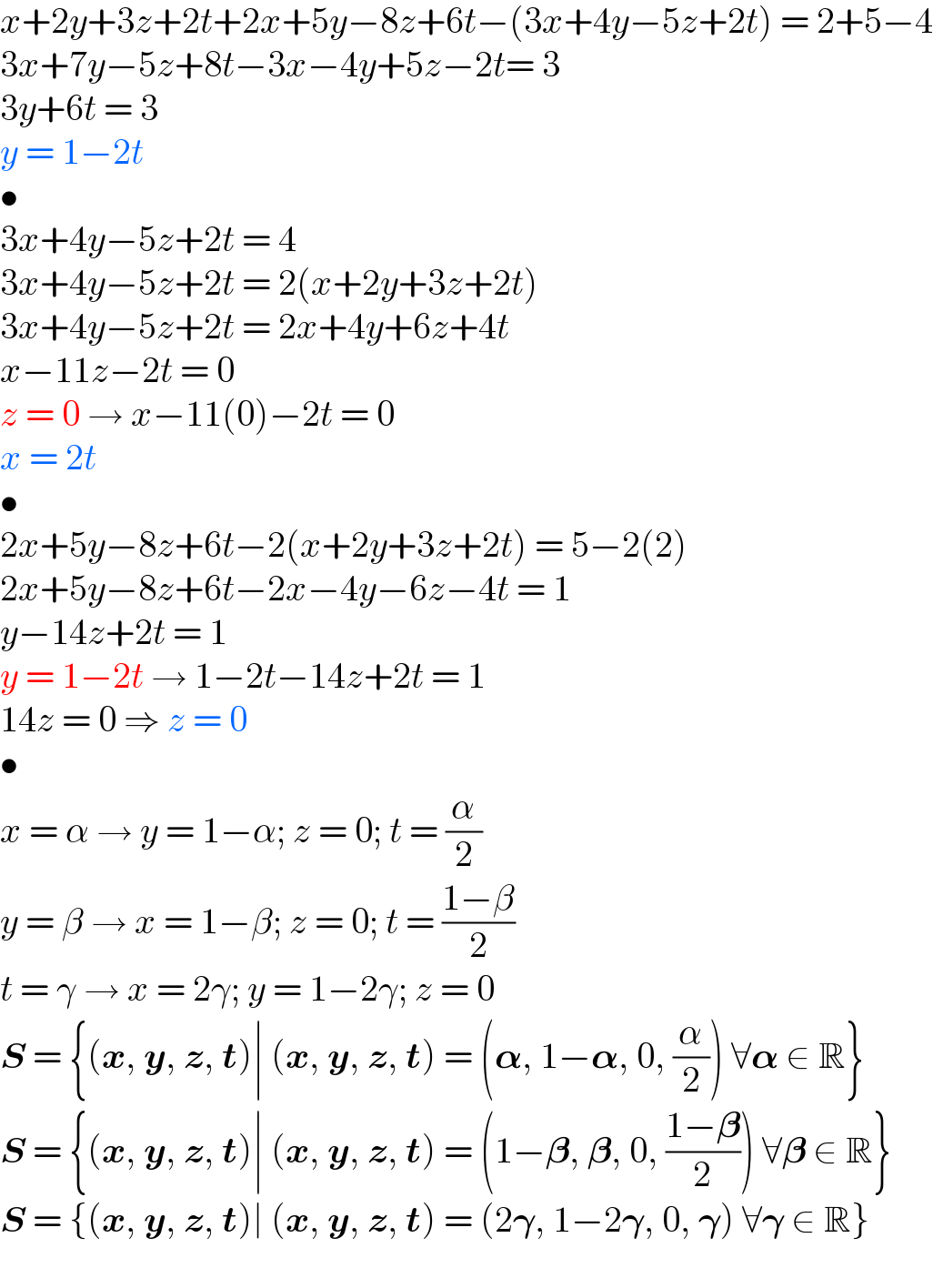
x+2y+3z+2t+2x+5y−8z+6t−(3x+4y−5z+2t) = 2+5−4 3x+7y−5z+8t−3x−4y+5z−2t= 3 3y+6t = 3 y = 1−2t • 3x+4y−5z+2t = 4 3x+4y−5z+2t = 2(x+2y+3z+2t) 3x+4y−5z+2t = 2x+4y+6z+4t x−11z−2t = 0 z = 0 → x−11(0)−2t = 0 x = 2t • 2x+5y−8z+6t−2(x+2y+3z+2t) = 5−2(2) 2x+5y−8z+6t−2x−4y−6z−4t = 1 y−14z+2t = 1 y = 1−2t → 1−2t−14z+2t = 1 14z = 0 ⇒ z = 0 • x = α → y = 1−α; z = 0; t = (α/2) y = β → x = 1−β; z = 0; t = ((1−β)/2) t = γ → x = 2γ; y = 1−2γ; z = 0 S = {(x, y, z, t)∣ (x, y, z, t) = (𝛂, 1−𝛂, 0, (α/2)) ∀𝛂 ∈ R} S = {(x, y, z, t)∣ (x, y, z, t) = (1−𝛃, 𝛃, 0, ((1−𝛃)/2)) ∀𝛃 ∈ R} S = {(x, y, z, t)∣ (x, y, z, t) = (2𝛄, 1−2𝛄, 0, 𝛄) ∀𝛄 ∈ R}

$${x}+\mathrm{2}{y}+\mathrm{3}{z}+\mathrm{2}{t}+\mathrm{2}{x}+\mathrm{5}{y}−\mathrm{8}{z}+\mathrm{6}{t}−\left(\mathrm{3}{x}+\mathrm{4}{y}−\mathrm{5}{z}+\mathrm{2}{t}\right)\:=\:\mathrm{2}+\mathrm{5}−\mathrm{4} \\ $$$$\mathrm{3}{x}+\mathrm{7}{y}−\mathrm{5}{z}+\mathrm{8}{t}−\mathrm{3}{x}−\mathrm{4}{y}+\mathrm{5}{z}−\mathrm{2}{t}=\:\mathrm{3} \\ $$$$\mathrm{3}{y}+\mathrm{6}{t}\:=\:\mathrm{3} \\ $$$${y}\:=\:\mathrm{1}−\mathrm{2}{t} \\ $$$$\bullet \\ $$$$\mathrm{3}{x}+\mathrm{4}{y}−\mathrm{5}{z}+\mathrm{2}{t}\:=\:\mathrm{4} \\ $$$$\mathrm{3}{x}+\mathrm{4}{y}−\mathrm{5}{z}+\mathrm{2}{t}\:=\:\mathrm{2}\left({x}+\mathrm{2}{y}+\mathrm{3}{z}+\mathrm{2}{t}\right) \\ $$$$\mathrm{3}{x}+\mathrm{4}{y}−\mathrm{5}{z}+\mathrm{2}{t}\:=\:\mathrm{2}{x}+\mathrm{4}{y}+\mathrm{6}{z}+\mathrm{4}{t} \\ $$$${x}−\mathrm{11}{z}−\mathrm{2}{t}\:=\:\mathrm{0} \\ $$$${z}\:=\:\mathrm{0}\:\rightarrow\:{x}−\mathrm{11}\left(\mathrm{0}\right)−\mathrm{2}{t}\:=\:\mathrm{0} \\ $$$${x}\:=\:\mathrm{2}{t} \\ $$$$\bullet \\ $$$$\mathrm{2}{x}+\mathrm{5}{y}−\mathrm{8}{z}+\mathrm{6}{t}−\mathrm{2}\left({x}+\mathrm{2}{y}+\mathrm{3}{z}+\mathrm{2}{t}\right)\:=\:\mathrm{5}−\mathrm{2}\left(\mathrm{2}\right) \\ $$$$\mathrm{2}{x}+\mathrm{5}{y}−\mathrm{8}{z}+\mathrm{6}{t}−\mathrm{2}{x}−\mathrm{4}{y}−\mathrm{6}{z}−\mathrm{4}{t}\:=\:\mathrm{1} \\ $$$${y}−\mathrm{14}{z}+\mathrm{2}{t}\:=\:\mathrm{1} \\ $$$${y}\:=\:\mathrm{1}−\mathrm{2}{t}\:\rightarrow\:\mathrm{1}−\mathrm{2}{t}−\mathrm{14}{z}+\mathrm{2}{t}\:=\:\mathrm{1} \\ $$$$\mathrm{14}{z}\:=\:\mathrm{0}\:\Rightarrow\:{z}\:=\:\mathrm{0} \\ $$$$\bullet \\ $$$${x}\:=\:\alpha\:\rightarrow\:{y}\:=\:\mathrm{1}−\alpha;\:{z}\:=\:\mathrm{0};\:{t}\:=\:\frac{\alpha}{\mathrm{2}} \\ $$$${y}\:=\:\beta\:\rightarrow\:{x}\:=\:\mathrm{1}−\beta;\:{z}\:=\:\mathrm{0};\:{t}\:=\:\frac{\mathrm{1}−\beta}{\mathrm{2}} \\ $$$${t}\:=\:\gamma\:\rightarrow\:{x}\:=\:\mathrm{2}\gamma;\:{y}\:=\:\mathrm{1}−\mathrm{2}\gamma;\:{z}\:=\:\mathrm{0} \\ $$$$\boldsymbol{{S}}\:=\:\left\{\left(\boldsymbol{{x}},\:\boldsymbol{{y}},\:\boldsymbol{{z}},\:\boldsymbol{{t}}\right)\mid\:\left(\boldsymbol{{x}},\:\boldsymbol{{y}},\:\boldsymbol{{z}},\:\boldsymbol{{t}}\right)\:=\:\left(\boldsymbol{\alpha},\:\mathrm{1}−\boldsymbol{\alpha},\:\mathrm{0},\:\frac{\alpha}{\mathrm{2}}\right)\:\forall\boldsymbol{\alpha}\:\in\:\mathbb{R}\right\} \\ $$$$\boldsymbol{{S}}\:=\:\left\{\left(\boldsymbol{{x}},\:\boldsymbol{{y}},\:\boldsymbol{{z}},\:\boldsymbol{{t}}\right)\mid\:\left(\boldsymbol{{x}},\:\boldsymbol{{y}},\:\boldsymbol{{z}},\:\boldsymbol{{t}}\right)\:=\:\left(\mathrm{1}−\boldsymbol{\beta},\:\boldsymbol{\beta},\:\mathrm{0},\:\frac{\mathrm{1}−\boldsymbol{\beta}}{\mathrm{2}}\right)\:\forall\boldsymbol{\beta}\:\in\:\mathbb{R}\right\} \\ $$$$\boldsymbol{{S}}\:=\:\left\{\left(\boldsymbol{{x}},\:\boldsymbol{{y}},\:\boldsymbol{{z}},\:\boldsymbol{{t}}\right)\mid\:\left(\boldsymbol{{x}},\:\boldsymbol{{y}},\:\boldsymbol{{z}},\:\boldsymbol{{t}}\right)\:=\:\left(\mathrm{2}\boldsymbol{\gamma},\:\mathrm{1}−\mathrm{2}\boldsymbol{\gamma},\:\mathrm{0},\:\boldsymbol{\gamma}\right)\:\forall\boldsymbol{\gamma}\:\in\:\mathbb{R}\right\} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com