
Question Number 135692 by liberty last updated on 15/Mar/21

$$ \\ $$Solve the system of congruences 2x≡1(mod5) 3x≡2(mod7) 4x≡1(mod11)
Answered by floor(10²Eta[1]) last updated on 15/Mar/21
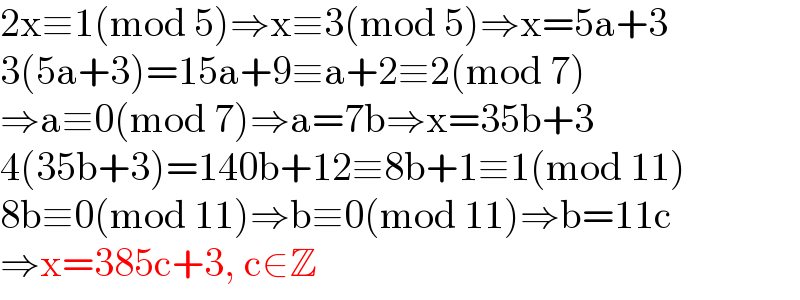
$$\mathrm{2x}\equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{5}\right)\Rightarrow\mathrm{x}\equiv\mathrm{3}\left(\mathrm{mod}\:\mathrm{5}\right)\Rightarrow\mathrm{x}=\mathrm{5a}+\mathrm{3} \\ $$$$\mathrm{3}\left(\mathrm{5a}+\mathrm{3}\right)=\mathrm{15a}+\mathrm{9}\equiv\mathrm{a}+\mathrm{2}\equiv\mathrm{2}\left(\mathrm{mod}\:\mathrm{7}\right) \\ $$$$\Rightarrow\mathrm{a}\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{7}\right)\Rightarrow\mathrm{a}=\mathrm{7b}\Rightarrow\mathrm{x}=\mathrm{35b}+\mathrm{3} \\ $$$$\mathrm{4}\left(\mathrm{35b}+\mathrm{3}\right)=\mathrm{140b}+\mathrm{12}\equiv\mathrm{8b}+\mathrm{1}\equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{11}\right) \\ $$$$\mathrm{8b}\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{11}\right)\Rightarrow\mathrm{b}\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{11}\right)\Rightarrow\mathrm{b}=\mathrm{11c} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{385c}+\mathrm{3},\:\mathrm{c}\in\mathbb{Z} \\ $$
Commented by liberty last updated on 15/Mar/21

$${thank}\:{you} \\ $$
