
Question Number 24864 by A1B1C1D1 last updated on 27/Nov/17

$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{following}\:\mathrm{trigonometric}\:\mathrm{limit}: \\ $$$$ \\ $$$$\underset{\mathrm{x}\:\rightarrow\:\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\:\left(\mathrm{5tg}\left(\mathrm{x}\right)\right)\:=\: \\ $$
Answered by jota+ last updated on 28/Nov/17
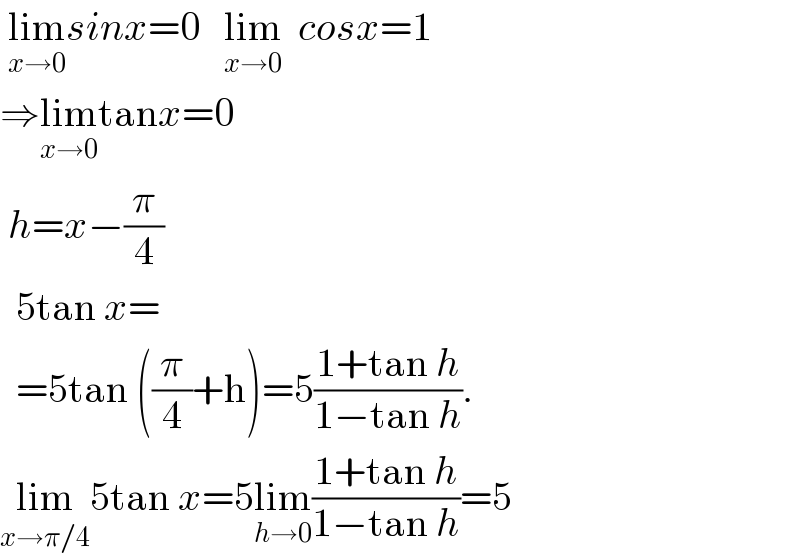
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{sinx}=\mathrm{0}\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:{cosx}=\mathrm{1} \\ $$$$\Rightarrow\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}tan}{x}=\mathrm{0}\: \\ $$$$\:{h}={x}−\frac{\pi}{\mathrm{4}} \\ $$$$\:\:\mathrm{5tan}\:{x}= \\ $$$$\:\:=\mathrm{5tan}\:\left(\frac{\pi}{\mathrm{4}}+\mathrm{h}\right)=\mathrm{5}\frac{\mathrm{1}+\mathrm{tan}\:{h}}{\mathrm{1}−\mathrm{tan}\:{h}}. \\ $$$$\underset{{x}\rightarrow\pi/\mathrm{4}} {\mathrm{lim}5tan}\:{x}=\mathrm{5}\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}+\mathrm{tan}\:{h}}{\mathrm{1}−\mathrm{tan}\:{h}}=\mathrm{5} \\ $$
