Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 13986 by RasheedSindhi last updated on 26/May/17

Solve the following system of equations. (x^2 /(√x))+((√y)/y^2 )=((1729)/(64)) (y^2 /(√x))−((√y)/x^2 )=((6908)/(81))

$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{following}\:\mathrm{system} \\ $$$$\mathrm{of}\:\mathrm{equations}. \\ $$$$\:\:\:\:\:\:\:\:\frac{\mathrm{x}^{\mathrm{2}} }{\sqrt{\mathrm{x}}}+\frac{\sqrt{\mathrm{y}}}{\mathrm{y}^{\mathrm{2}} }=\frac{\mathrm{1729}}{\mathrm{64}} \\ $$$$\:\:\:\:\:\:\:\:\frac{\mathrm{y}^{\mathrm{2}} }{\sqrt{\mathrm{x}}}−\frac{\sqrt{\mathrm{y}}}{\mathrm{x}^{\mathrm{2}} }=\frac{\mathrm{6908}}{\mathrm{81}} \\ $$$$ \\ $$

Commented by ajfour last updated on 27/May/17

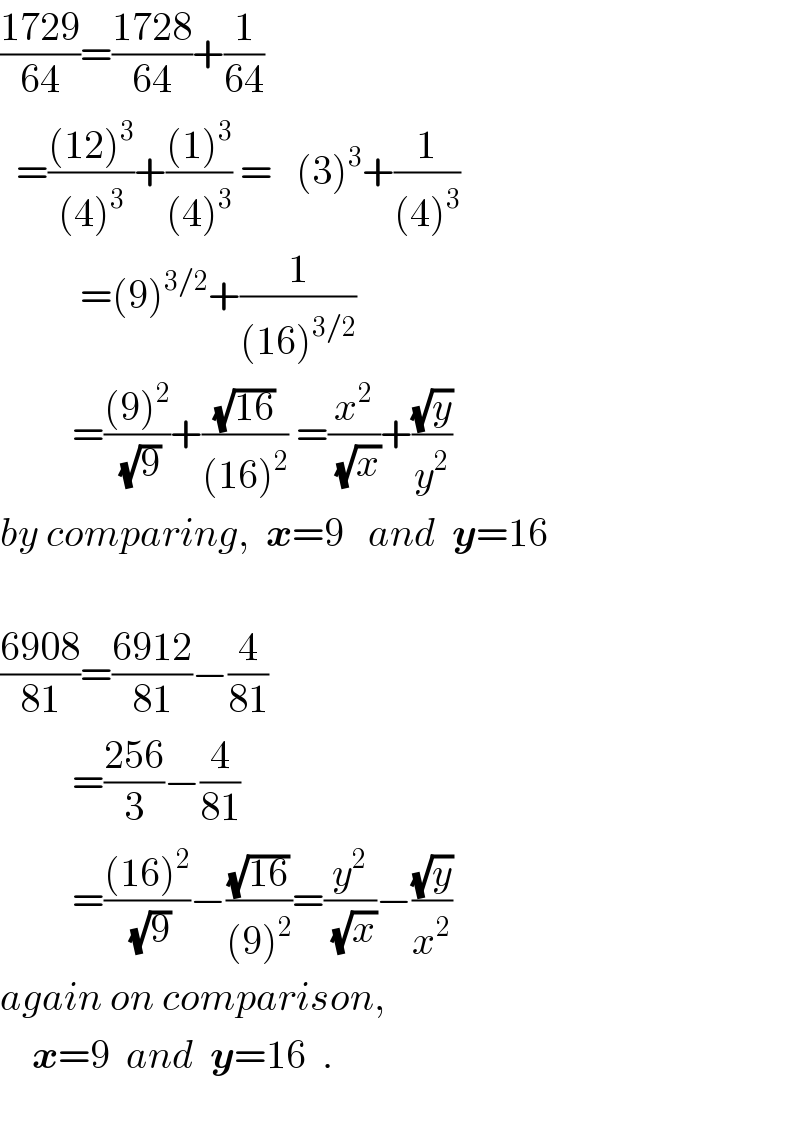
((1729)/(64))=((1728)/(64))+(1/(64)) =(((12)^3 )/((4)^3 ))+(((1)^3 )/((4)^3 )) = (3)^3 +(1/((4)^3 )) =(9)^(3/2) +(1/((16)^(3/2) )) =(((9)^2 )/(√9))+((√(16))/((16)^2 )) =(x^2 /(√x))+((√y)/y^2 ) by comparing, x=9 and y=16 ((6908)/(81))=((6912)/(81))−(4/(81)) =((256)/3)−(4/(81)) =(((16)^2 )/(√9))−((√(16))/((9)^2 ))=(y^2 /(√x))−((√y)/x^2 ) again on comparison, x=9 and y=16 .

$$\frac{\mathrm{1729}}{\mathrm{64}}=\frac{\mathrm{1728}}{\mathrm{64}}+\frac{\mathrm{1}}{\mathrm{64}} \\ $$$$\:\:=\frac{\left(\mathrm{12}\right)^{\mathrm{3}} }{\left(\mathrm{4}\right)^{\mathrm{3}} }+\frac{\left(\mathrm{1}\right)^{\mathrm{3}} }{\left(\mathrm{4}\right)^{\mathrm{3}} }\:=\:\:\:\left(\mathrm{3}\right)^{\mathrm{3}} +\frac{\mathrm{1}}{\left(\mathrm{4}\right)^{\mathrm{3}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{9}\right)^{\mathrm{3}/\mathrm{2}} +\frac{\mathrm{1}}{\left(\mathrm{16}\right)^{\mathrm{3}/\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\left(\mathrm{9}\right)^{\mathrm{2}} }{\sqrt{\mathrm{9}}}+\frac{\sqrt{\mathrm{16}}}{\left(\mathrm{16}\right)^{\mathrm{2}} }\:=\frac{{x}^{\mathrm{2}} }{\sqrt{{x}}}+\frac{\sqrt{{y}}}{{y}^{\mathrm{2}} } \\ $$$${by}\:{comparing},\:\:\boldsymbol{{x}}=\mathrm{9}\:\:\:{and}\:\:\boldsymbol{{y}}=\mathrm{16}\: \\ $$$$ \\ $$$$\frac{\mathrm{6908}}{\mathrm{81}}=\frac{\mathrm{6912}}{\mathrm{81}}−\frac{\mathrm{4}}{\mathrm{81}} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{256}}{\mathrm{3}}−\frac{\mathrm{4}}{\mathrm{81}}\: \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\left(\mathrm{16}\right)^{\mathrm{2}} }{\sqrt{\mathrm{9}}}−\frac{\sqrt{\mathrm{16}}}{\left(\mathrm{9}\right)^{\mathrm{2}} }=\frac{{y}^{\mathrm{2}} }{\sqrt{{x}}}−\frac{\sqrt{{y}}}{{x}^{\mathrm{2}} }\: \\ $$$${again}\:{on}\:{comparison}, \\ $$$$\:\:\:\:\boldsymbol{{x}}=\mathrm{9}\:\:{and}\:\:\boldsymbol{{y}}=\mathrm{16}\:\:. \\ $$$$ \\ $$

Commented by RasheedSindhi last updated on 27/May/17

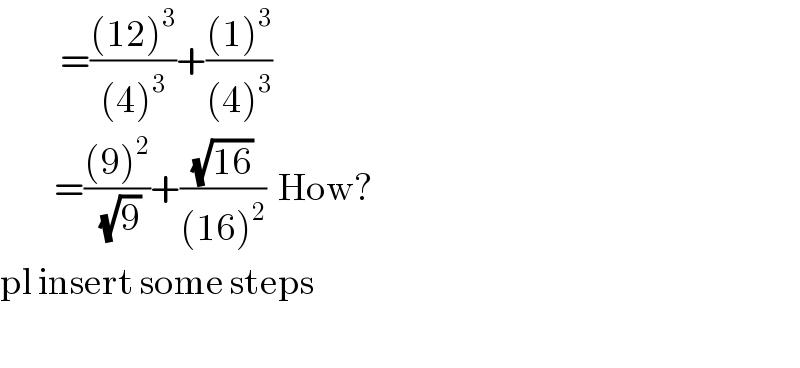
=(((12)^3 )/((4)^3 ))+(((1)^3 )/((4)^3 )) =(((9)^2 )/(√9))+((√(16))/((16)^2 )) How? pl insert some steps

$$\:\:\:\:\:\:\:\:\:\:=\frac{\left(\mathrm{12}\right)^{\mathrm{3}} }{\left(\mathrm{4}\right)^{\mathrm{3}} }+\frac{\left(\mathrm{1}\right)^{\mathrm{3}} }{\left(\mathrm{4}\right)^{\mathrm{3}} } \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\left(\mathrm{9}\right)^{\mathrm{2}} }{\sqrt{\mathrm{9}}}+\frac{\sqrt{\mathrm{16}}}{\left(\mathrm{16}\right)^{\mathrm{2}} }\:\:\mathrm{How}? \\ $$$$\mathrm{pl}\:\mathrm{insert}\:\mathrm{some}\:\mathrm{steps} \\ $$$$ \\ $$

Commented by ajfour last updated on 27/May/17

did . Sir !

$${did}\:.\:{Sir}\:! \\ $$

Commented by RasheedSindhi last updated on 27/May/17

θαnk you!

$$\theta\alpha{nk}\:{you}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com