
Question Number 197470 by Mastermind last updated on 18/Sep/23
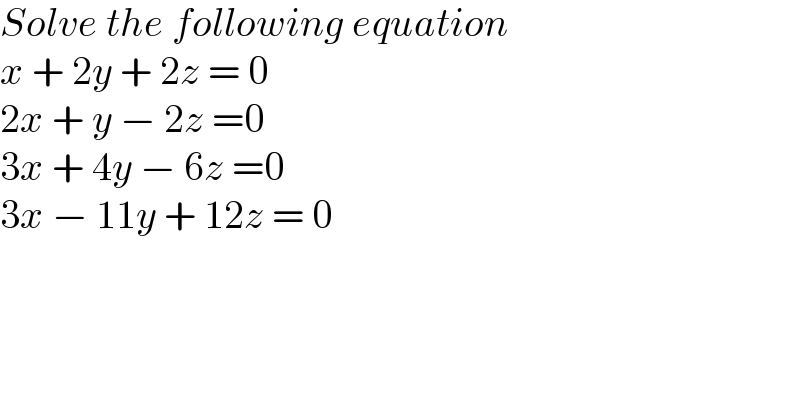
$${Solve}\:{the}\:{following}\:{equation} \\ $$$${x}\:+\:\mathrm{2}{y}\:+\:\mathrm{2}{z}\:=\:\mathrm{0} \\ $$$$\mathrm{2}{x}\:+\:{y}\:−\:\mathrm{2}{z}\:=\mathrm{0} \\ $$$$\mathrm{3}{x}\:+\:\mathrm{4}{y}\:−\:\mathrm{6}{z}\:=\mathrm{0} \\ $$$$\mathrm{3}{x}\:−\:\mathrm{11}{y}\:+\:\mathrm{12}{z}\:=\:\mathrm{0} \\ $$
Answered by MathedUp last updated on 19/Sep/23
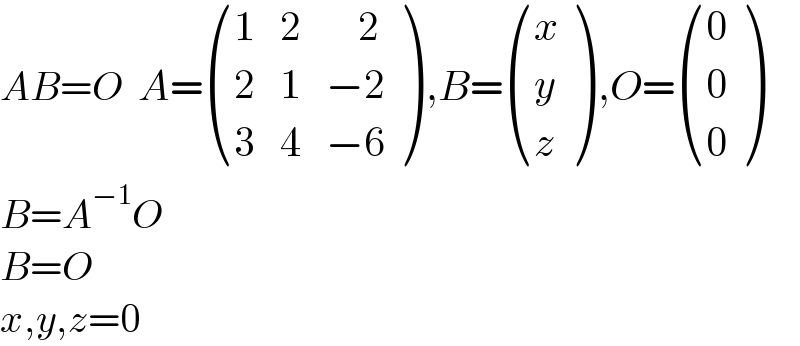
$${AB}={O}\:\:{A}=\begin{pmatrix}{\mathrm{1}}&{\mathrm{2}}&{\:\:\:\:\mathrm{2}}\\{\mathrm{2}}&{\mathrm{1}}&{−\mathrm{2}}\\{\mathrm{3}}&{\mathrm{4}}&{−\mathrm{6}}\end{pmatrix}\:,{B}=\begin{pmatrix}{{x}}\\{{y}}\\{{z}}\end{pmatrix}\:,{O}=\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix} \\ $$$${B}={A}^{−\mathrm{1}} {O} \\ $$$${B}={O} \\ $$$${x},{y},{z}=\mathrm{0} \\ $$
Commented by Mastermind last updated on 25/Sep/23
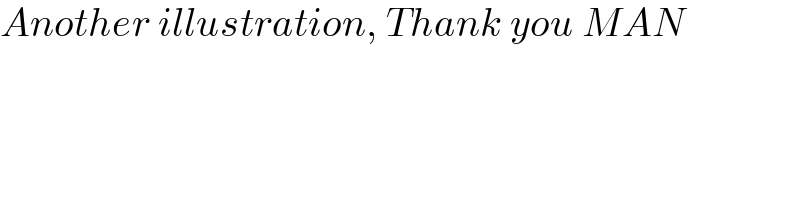
$${Another}\:{illustration},\:{Thank}\:{you}\:{MAN} \\ $$
Answered by deleteduser1 last updated on 18/Sep/23
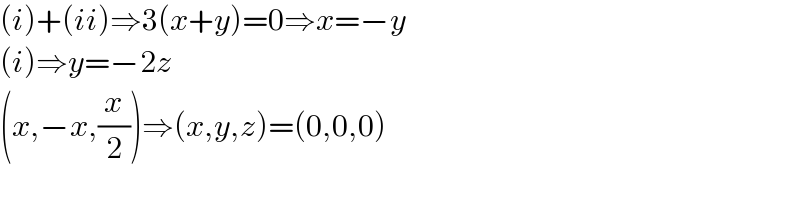
$$\left({i}\right)+\left({ii}\right)\Rightarrow\mathrm{3}\left({x}+{y}\right)=\mathrm{0}\Rightarrow{x}=−{y} \\ $$$$\left({i}\right)\Rightarrow{y}=−\mathrm{2}{z} \\ $$$$\left({x},−{x},\frac{{x}}{\mathrm{2}}\right)\Rightarrow\left({x},{y},{z}\right)=\left(\mathrm{0},\mathrm{0},\mathrm{0}\right) \\ $$
Commented by Mastermind last updated on 18/Sep/23
$${Thank}\:{you}\:{so}\:{much}\:{BOSS} \\ $$
