
Previous in Differential Equation Next in Differential Equation
Question Number 84232 by niroj last updated on 10/Mar/20
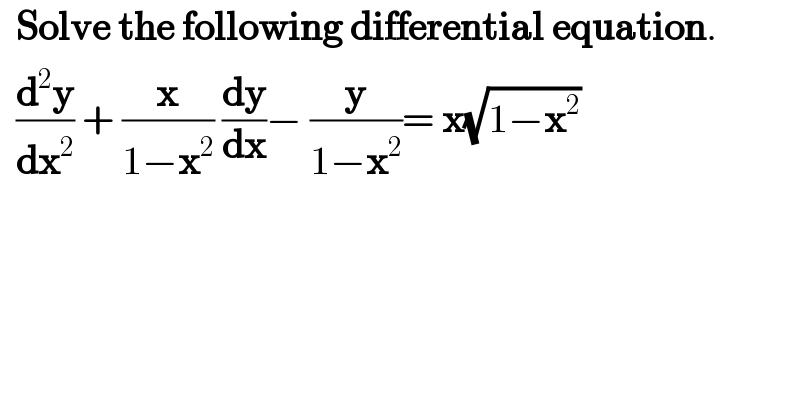
$$\:\:\boldsymbol{\mathrm{Solve}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{following}}\:\boldsymbol{\mathrm{differential}}\:\boldsymbol{\mathrm{equation}}. \\ $$$$\:\:\frac{\boldsymbol{\mathrm{d}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}}{\boldsymbol{\mathrm{dx}}^{\mathrm{2}} }\:+\:\frac{\boldsymbol{\mathrm{x}}}{\mathrm{1}−\boldsymbol{\mathrm{x}}^{\mathrm{2}} }\:\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{dx}}}−\:\frac{\boldsymbol{\mathrm{y}}}{\mathrm{1}−\boldsymbol{\mathrm{x}}^{\mathrm{2}} }=\:\boldsymbol{\mathrm{x}}\sqrt{\mathrm{1}−\boldsymbol{\mathrm{x}}^{\mathrm{2}} } \\ $$
Commented by mind is power last updated on 11/Mar/20
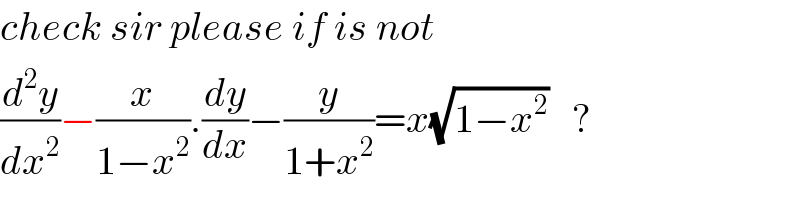
$${check}\:{sir}\:{please}\:{if}\:{is}\:{not}\: \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }−\frac{{x}}{\mathrm{1}−{x}^{\mathrm{2}} }.\frac{{dy}}{{dx}}−\frac{{y}}{\mathrm{1}+{x}^{\mathrm{2}} }={x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:\:\:? \\ $$
Commented by niroj last updated on 11/Mar/20
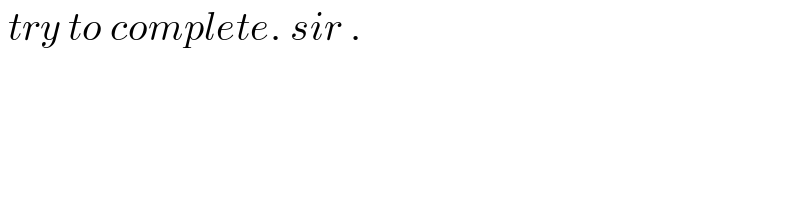
$$\:{try}\:{to}\:{complete}.\:{sir}\:. \\ $$
Answered by mind is power last updated on 11/Mar/20

$${if} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }−\frac{{x}}{\mathrm{1}−{x}^{\mathrm{2}} }.\frac{{dy}}{{dx}}−\frac{{y}}{\mathrm{1}−{x}^{\mathrm{2}} }={x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$${x}={sin}\left({t}\right)\Rightarrow{y}\left({x}\right)={y}\left({sin}\left({t}\right)\right)={z}\left({t}\right) \\ $$$$\frac{{dy}}{{dx}}=\frac{{d}}{{dt}}{y}\left({sin}\left({t}\right)\right).\frac{\mathrm{1}}{\frac{{dx}}{{dt}}}={z}'\left({t}\right).\frac{\mathrm{1}}{{cos}\left({t}\right)} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{{z}''{cos}\left({t}\right)+{sin}\left({t}\right){z}'}{{cos}^{\mathrm{2}} \left({t}\right)}.\frac{\mathrm{1}}{{cos}\left({t}\right)} \\ $$$$\Rightarrow\frac{{z}''{cos}\left({t}\right)+{sin}\left({t}\right){z}'}{{cos}^{\mathrm{3}} \left({t}\right)}−\frac{{sin}\left({t}\right)}{{cos}^{\mathrm{2}} \left({t}\right)}.\frac{{z}'\left({t}\right)}{{cos}\left({t}\right)}−\frac{{z}}{{cos}^{\mathrm{2}} \left({t}\right)}={sin}\left({t}\right){cos}\left({t}\right) \\ $$$$\Leftrightarrow{z}''−{z}={sin}\left({t}\right){cos}^{\mathrm{3}} \left({t}\right)=\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}{t}\right)\left(\frac{\mathrm{1}+{cos}\left(\mathrm{2}{t}\right)}{\mathrm{2}}\right) \\ $$$$\Rightarrow{z}''−{z}=\frac{{sin}\left(\mathrm{2}{t}\right)}{\mathrm{4}}+\frac{{sin}\left(\mathrm{4}{t}\right)}{\mathrm{8}} \\ $$$${z}\left({t}\right)={se}^{{t}} +{be}^{−{t}} \:\:{for}\:{homgenius}\:{equation} \\ $$$${z}_{\mathrm{1}} =\frac{−{sin}\left(\mathrm{2}{t}\right)}{\mathrm{20}}−\frac{{sin}\left(\mathrm{4}{t}\right)}{\mathrm{136}}\:{particular}\:{solution} \\ $$$${z}\left({t}\right)={se}^{{t}} +{be}^{−{t}} −\frac{{sin}\left(\mathrm{2}{t}\right)}{\mathrm{20}}−\frac{{sin}\left(\mathrm{4}{t}\right)}{\mathrm{136}} \\ $$$${t}={arcsin}\left({x}\right) \\ $$$${z}\left({t}\right)={z}\left({arcsin}\left({x}\right)\right)={y}\left({x}\right) \\ $$$${y}\left({x}\right)={se}^{{arcsin}\left({x}\right)} +{be}^{−{arcsin}\left({x}\right)} −\frac{{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{\mathrm{10}}−\frac{{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }.\left(\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} \right)}{\mathrm{34}} \\ $$
