
Question Number 154497 by mathdanisur last updated on 18/Sep/21
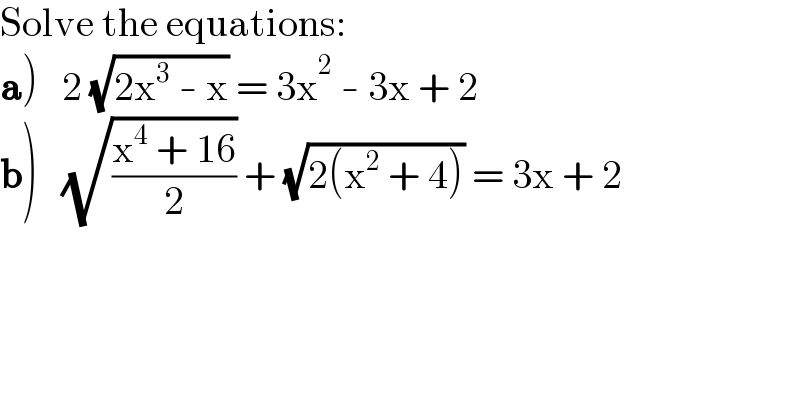
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{equations}: \\ $$$$\left.\boldsymbol{\mathrm{a}}\right)\:\:\:\mathrm{2}\:\sqrt{\mathrm{2x}^{\mathrm{3}} \:-\:\mathrm{x}}\:=\:\mathrm{3x}^{\mathrm{2}} \:-\:\mathrm{3x}\:+\:\mathrm{2} \\ $$$$\left.\boldsymbol{\mathrm{b}}\right)\:\:\:\sqrt{\frac{\mathrm{x}^{\mathrm{4}} \:+\:\mathrm{16}}{\mathrm{2}}}\:+\:\sqrt{\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{4}\right)}\:=\:\mathrm{3x}\:+\:\mathrm{2} \\ $$
Answered by ARUNG_Brandon_MBU last updated on 18/Sep/21
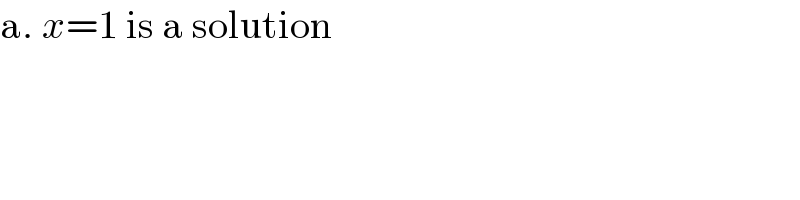
$$\mathrm{a}.\:{x}=\mathrm{1}\:\mathrm{is}\:\mathrm{a}\:\mathrm{solution} \\ $$
Answered by Fridunatjan08 last updated on 19/Sep/21
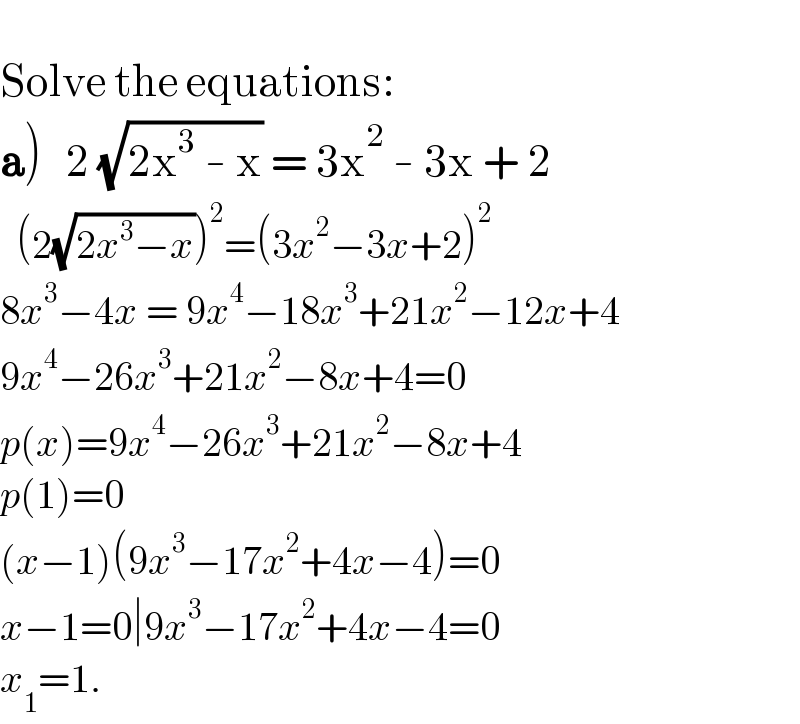
$$ \\ $$$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{equations}: \\ $$$$\left.\boldsymbol{\mathrm{a}}\right)\:\:\:\mathrm{2}\:\sqrt{\mathrm{2x}^{\mathrm{3}} \:-\:\mathrm{x}}\:=\:\mathrm{3x}^{\mathrm{2}} \:-\:\mathrm{3x}\:+\:\mathrm{2} \\ $$$$\:\:\left(\mathrm{2}\sqrt{\mathrm{2}{x}^{\mathrm{3}} −{x}}\right)^{\mathrm{2}} =\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}\right)^{\mathrm{2}} \\ $$$$\mathrm{8}{x}^{\mathrm{3}} −\mathrm{4}{x}\:=\:\mathrm{9}{x}^{\mathrm{4}} −\mathrm{18}{x}^{\mathrm{3}} +\mathrm{21}{x}^{\mathrm{2}} −\mathrm{12}{x}+\mathrm{4} \\ $$$$\mathrm{9}{x}^{\mathrm{4}} −\mathrm{26}{x}^{\mathrm{3}} +\mathrm{21}{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{4}=\mathrm{0} \\ $$$${p}\left({x}\right)=\mathrm{9}{x}^{\mathrm{4}} −\mathrm{26}{x}^{\mathrm{3}} +\mathrm{21}{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{4} \\ $$$${p}\left(\mathrm{1}\right)=\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)\left(\mathrm{9}{x}^{\mathrm{3}} −\mathrm{17}{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{4}\right)=\mathrm{0} \\ $$$${x}−\mathrm{1}=\mathrm{0}\mid\mathrm{9}{x}^{\mathrm{3}} −\mathrm{17}{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{4}=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =\mathrm{1}. \\ $$
Commented by mathdanisur last updated on 19/Sep/21
$$\mathrm{Very}\:\mathrm{nice}\:\mathrm{Ser}\:\mathrm{thanks} \\ $$
