Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 132632 by mohammad17 last updated on 15/Feb/21

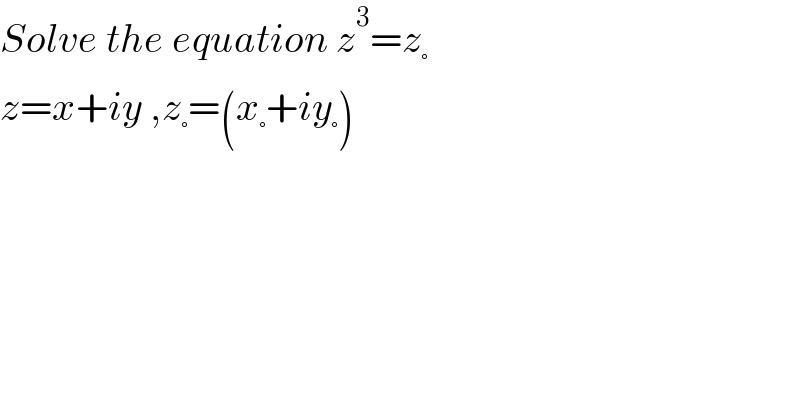
Solve the equation z^3 =z_° z=x+iy ,z_° =(x_° +iy_° )

$${Solve}\:{the}\:{equation}\:{z}^{\mathrm{3}} ={z}_{°} \\ $$$${z}={x}+{iy}\:,{z}_{°} =\left({x}_{°} +{iy}_{°} \right) \\ $$

Answered by TheSupreme last updated on 15/Feb/21

x_0 +iy_0 =ρe^(iθ) ρ=(√(x_0 ^2 +y_0 ^2 )) tan(θ)=(y_0 /x_0 ) we have to correct phase θ=atan((x_0 /y_0 ))+π sgn(x_0 ) z=z_0 ^(1/3) =ρ^(1/3) e^(i ((θ+2nπ)/3)) z_n =(x_0 ^2 +y_0 ^2 )^(1/6) e^(i((atan((x_0 /y_0 ))+π(2n+sgn(x_0 )))/3)) i=0,1,2

$${x}_{\mathrm{0}} +{iy}_{\mathrm{0}} =\rho{e}^{{i}\theta} \:\rho=\sqrt{{x}_{\mathrm{0}} ^{\mathrm{2}} +{y}_{\mathrm{0}} ^{\mathrm{2}} }\:{tan}\left(\theta\right)=\frac{{y}_{\mathrm{0}} }{{x}_{\mathrm{0}} } \\ $$$${we}\:{have}\:{to}\:{correct}\:{phase} \\ $$$$\theta={atan}\left(\frac{{x}_{\mathrm{0}} }{{y}_{\mathrm{0}} }\right)+\pi\:{sgn}\left({x}_{\mathrm{0}} \right) \\ $$$${z}={z}_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} =\rho^{\frac{\mathrm{1}}{\mathrm{3}}} {e}^{{i}\:\frac{\theta+\mathrm{2}{n}\pi}{\mathrm{3}}} \\ $$$${z}_{{n}} =\left({x}_{\mathrm{0}} ^{\mathrm{2}} +{y}_{\mathrm{0}} ^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{6}}} {e}^{{i}\frac{{atan}\left(\frac{{x}_{\mathrm{0}} }{{y}_{\mathrm{0}} }\right)+\pi\left(\mathrm{2}{n}+{sgn}\left({x}_{\mathrm{0}} \right)\right)}{\mathrm{3}}} \:{i}=\mathrm{0},\mathrm{1},\mathrm{2} \\ $$$$ \\ $$

Commented by mohammad17 last updated on 15/Feb/21

sir can you give me defintion of sgn please

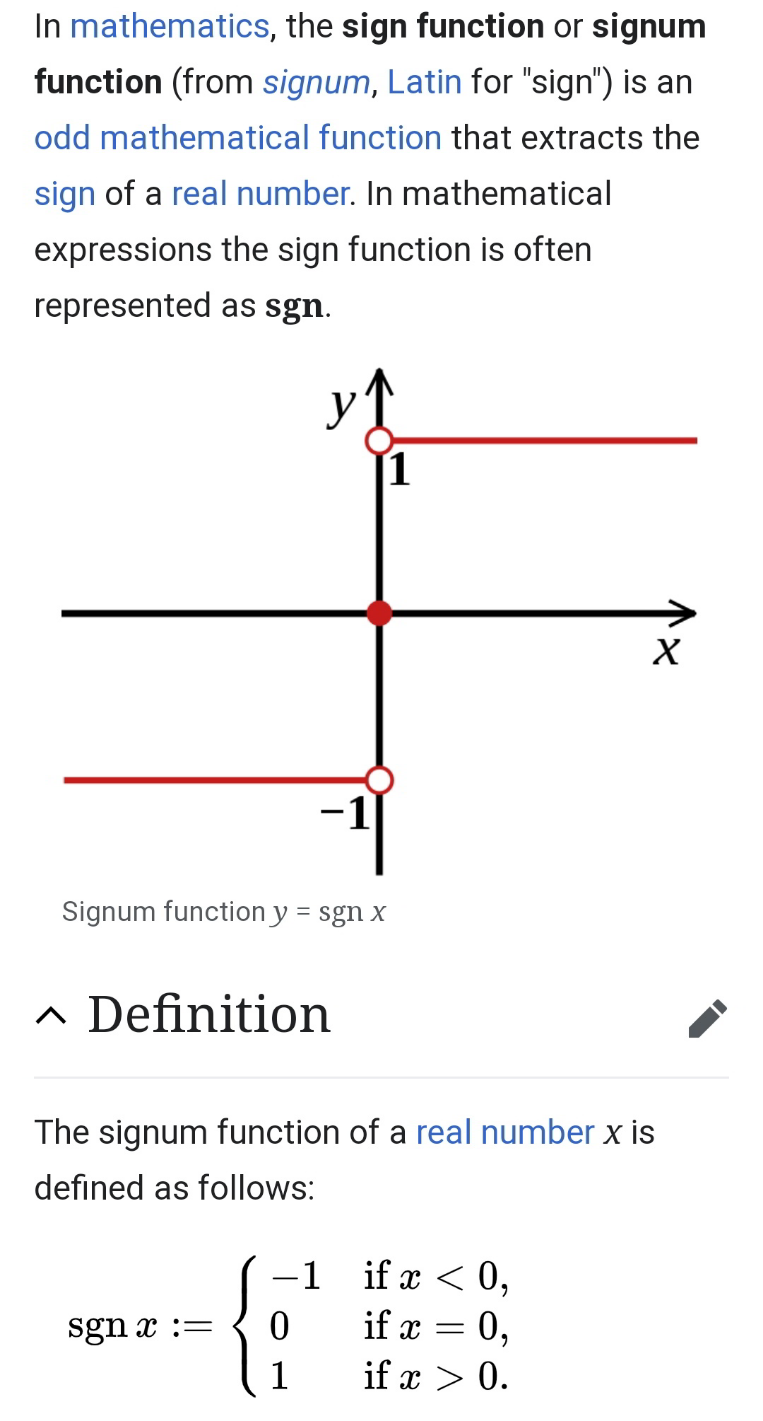
$${sir}\:{can}\:{you}\:{give}\:{me}\:{defintion}\:{of}\:{sgn}\:{please} \\ $$

Commented by Ar Brandon last updated on 15/Feb/21

sgn(x)=sign of x

$$\mathrm{sgn}\left(\mathrm{x}\right)=\mathrm{sign}\:\mathrm{of}\:\mathrm{x} \\ $$

Commented by mr W last updated on 15/Feb/21

Terms of Service

Privacy Policy

Contact: info@tinkutara.com