
Question Number 197895 by tri26112004 last updated on 02/Oct/23
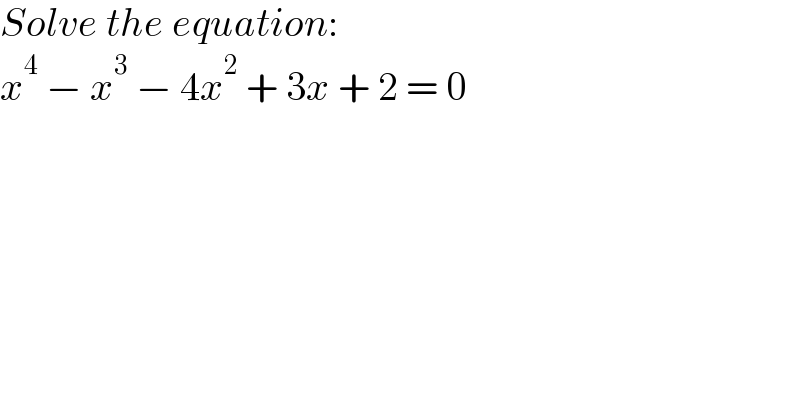
$${Solve}\:{the}\:{equation}: \\ $$$${x}^{\mathrm{4}} \:−\:{x}^{\mathrm{3}} \:−\:\mathrm{4}{x}^{\mathrm{2}} \:+\:\mathrm{3}{x}\:+\:\mathrm{2}\:=\:\mathrm{0} \\ $$
Answered by Frix last updated on 02/Oct/23

$$\left({x}−\mathrm{2}\right)\left({x}^{\mathrm{3}} +{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{1}\right)=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =\mathrm{2} \\ $$$$\mathrm{Use}\:\mathrm{trigonometric}\:\mathrm{method} \\ $$$${x}_{\mathrm{2}} =−\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{7}}\mathrm{cos}\:\frac{\pi+\mathrm{2sin}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{7}}}{\mathrm{14}}}{\mathrm{6}}}{\mathrm{3}} \\ $$$${x}_{\mathrm{3}} =−\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{7}}\mathrm{sin}\:\frac{\mathrm{sin}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{7}}}{\mathrm{14}}}{\mathrm{3}}}{\mathrm{3}} \\ $$$${x}_{\mathrm{4}} =\frac{−\mathrm{1}+\mathrm{2}\sqrt{\mathrm{7}}\mathrm{sin}\:\frac{\pi+\mathrm{sin}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{7}}}{\mathrm{14}}}{\mathrm{3}}}{\mathrm{3}} \\ $$
Commented by Frix last updated on 03/Oct/23
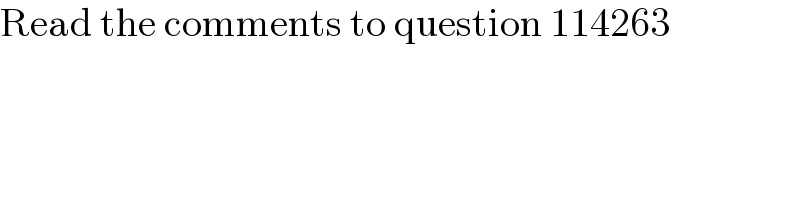
$$\mathrm{Read}\:\mathrm{the}\:\mathrm{comments}\:\mathrm{to}\:\mathrm{question}\:\mathrm{114263} \\ $$
Commented by tri26112004 last updated on 03/Oct/23
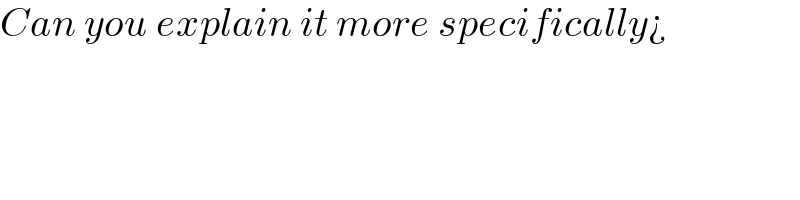
$${Can}\:{you}\:{explain}\:{it}\:{more}\:{specifically}¿ \\ $$
