Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 205471 by Fridunatjan08 last updated on 21/Mar/24

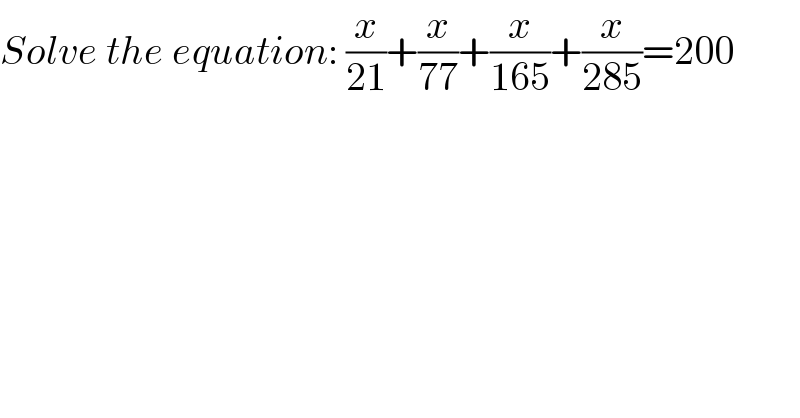
Solve the equation: (x/(21))+(x/(77))+(x/(165))+(x/(285))=200

$${Solve}\:{the}\:{equation}:\:\frac{{x}}{\mathrm{21}}+\frac{{x}}{\mathrm{77}}+\frac{{x}}{\mathrm{165}}+\frac{{x}}{\mathrm{285}}=\mathrm{200} \\ $$

Answered by Rasheed.Sindhi last updated on 23/Mar/24

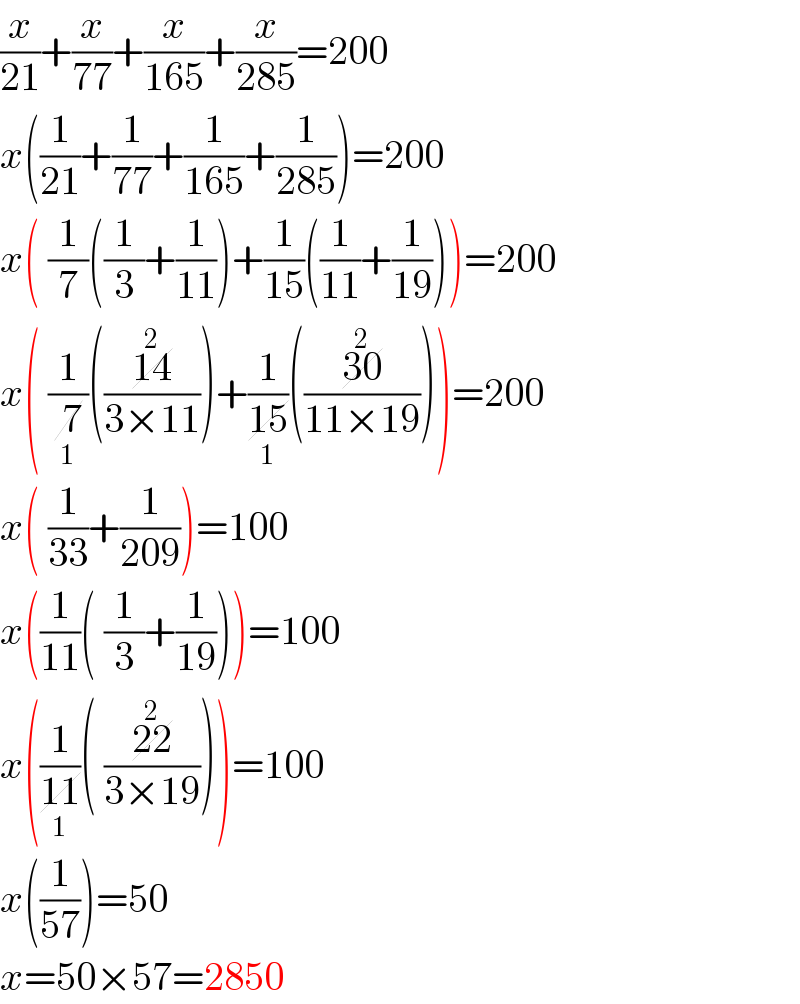
(x/(21))+(x/(77))+(x/(165))+(x/(285))=200 x((1/(21))+(1/(77))+(1/(165))+(1/(285)))=200 x( (1/7)((1/3)+(1/(11)))+(1/(15))((1/(11))+(1/(19))))=200 x( (1/( 7_(1) ))(((14^(2) )/(3×11)))+(1/(15_(1) ))(((30^(2) )/(11×19))))=200 x( (1/(33))+(1/(209)))=100 x((1/(11))( (1/3)+(1/(19))))=100 x((1/(11_(1) ))( ((22^(2) )/(3×19))))=100 x((1/(57)))=50 x=50×57=2850

$$\frac{{x}}{\mathrm{21}}+\frac{{x}}{\mathrm{77}}+\frac{{x}}{\mathrm{165}}+\frac{{x}}{\mathrm{285}}=\mathrm{200} \\ $$$${x}\left(\frac{\mathrm{1}}{\mathrm{21}}+\frac{\mathrm{1}}{\mathrm{77}}+\frac{\mathrm{1}}{\mathrm{165}}+\frac{\mathrm{1}}{\mathrm{285}}\right)=\mathrm{200} \\ $$$${x}\left(\:\frac{\mathrm{1}}{\mathrm{7}}\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{11}}\right)+\frac{\mathrm{1}}{\mathrm{15}}\left(\frac{\mathrm{1}}{\mathrm{11}}+\frac{\mathrm{1}}{\mathrm{19}}\right)\right)=\mathrm{200} \\ $$$${x}\left(\:\frac{\mathrm{1}}{\cancel{\underset{\mathrm{1}} {\:\mathrm{7}}}}\left(\frac{\cancel{\overset{\mathrm{2}} {\mathrm{14}}}}{\mathrm{3}×\mathrm{11}}\right)+\frac{\mathrm{1}}{\cancel{\underset{\mathrm{1}} {\mathrm{15}}}}\left(\frac{\cancel{\overset{\mathrm{2}} {\mathrm{30}}}}{\mathrm{11}×\mathrm{19}}\right)\right)=\mathrm{200} \\ $$$${x}\left(\:\frac{\mathrm{1}}{\mathrm{33}}+\frac{\mathrm{1}}{\mathrm{209}}\right)=\mathrm{100} \\ $$$${x}\left(\frac{\mathrm{1}}{\mathrm{11}}\left(\:\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{19}}\right)\right)=\mathrm{100} \\ $$$${x}\left(\frac{\mathrm{1}}{\cancel{\underset{\mathrm{1}} {\mathrm{11}}}}\left(\:\frac{\cancel{\overset{\mathrm{2}} {\mathrm{22}}}}{\mathrm{3}×\mathrm{19}}\right)\right)=\mathrm{100} \\ $$$${x}\left(\frac{\mathrm{1}}{\mathrm{57}}\right)=\mathrm{50} \\ $$$${x}=\mathrm{50}×\mathrm{57}=\mathrm{2850} \\ $$

Answered by Rasheed.Sindhi last updated on 22/Mar/24

Similar method(grouping in another way) (x/(21))+(x/(285))+(x/(77))+(x/(165))=200 (1/3)((x/7)+(x/(95)))+(1/(11))((x/7)+(x/(15)))=200 (1/3)∙((102^(34) x)/(665))+(1/(11))∙((22^(2) x)/(105))=200 ((17x)/(665))+(x/(105))=100 (1/(35))(((17x)/(19))+(x/3))=100 (1/(35))(((70^(2) x)/(57)))=100 (x/(57))=50⇒x=2850

$${Similar}\:{method}\left({grouping}\:{in}\:{another}\:{way}\right) \\ $$$$\frac{{x}}{\mathrm{21}}+\frac{{x}}{\mathrm{285}}+\frac{{x}}{\mathrm{77}}+\frac{{x}}{\mathrm{165}}=\mathrm{200} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{{x}}{\mathrm{7}}+\frac{{x}}{\mathrm{95}}\right)+\frac{\mathrm{1}}{\mathrm{11}}\left(\frac{{x}}{\mathrm{7}}+\frac{{x}}{\mathrm{15}}\right)=\mathrm{200} \\ $$$$\frac{\mathrm{1}}{\cancel{\mathrm{3}}}\centerdot\frac{\cancel{\overset{\mathrm{34}} {\mathrm{102}}}{x}}{\mathrm{665}}+\frac{\mathrm{1}}{\cancel{\mathrm{11}}}\centerdot\frac{\cancel{\overset{\mathrm{2}} {\mathrm{22}}}{x}}{\mathrm{105}}=\mathrm{200} \\ $$$$\:\:\:\:\:\frac{\mathrm{17}{x}}{\mathrm{665}}+\frac{{x}}{\mathrm{105}}=\mathrm{100} \\ $$$$\:\:\:\frac{\mathrm{1}}{\mathrm{35}}\left(\frac{\mathrm{17}{x}}{\mathrm{19}}+\frac{{x}}{\mathrm{3}}\right)=\mathrm{100} \\ $$$$\:\:\:\frac{\mathrm{1}}{\cancel{\mathrm{35}}}\left(\frac{\cancel{\overset{\mathrm{2}} {\mathrm{70}}}{x}}{\mathrm{57}}\right)=\mathrm{100} \\ $$$$\:\:\:\:\:\:\:\:\frac{{x}}{\mathrm{57}}=\mathrm{50}\Rightarrow{x}=\mathrm{2850} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com